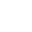2022-2023 春学期 矩阵与数值分析 C5 插值与逼近

C5 插值与逼近

5.1 引言

有 n 个插值节点，就有 n 插值条件，可以构造至多 n-1 次的插值函数

需要考虑简单函数类的选取问题： 如代数多项式， 三角多项式，分段多项式，有理函数，样条函数等；存在唯一性问题；余项估计问题；收敛性问题等

思想是：简单函数类的基底需满足条件；给出具体的基底；给出系数

解存在条件-Harr 条件：设 $\varphi_1(x),\varphi_2(x),\cdots,\varphi_n(x)$ 是 $[a,b]$ 上的函数，且对 上的任意 n 个互异点 $x_1,x_2,\cdots,x_n$，有行列式

$$\begin{vmatrix} \varphi_1(x_1)&\varphi_2(x_1)&\cdots&\varphi_n(x_1)\\ \varphi_1(x_2)&\varphi_2(x_2)&\cdots&\varphi_n(x_2)\\ \vdots&\vdots&\ddots&\vdots\\ \varphi_1(x_n)&\varphi_2(x_n)&\cdots&\varphi_n(x_n)\\ \end{vmatrix}$$

则称 $\varphi_1(x),\varphi_2(x),\cdots,\varphi_n(x)$ 在 $[a,b]$ 上满足 Haar 条件

解存在唯一性定理：设已知函数 $f(x)$ 在 n 个互异点 $x_1,x_2,\cdots,x_n$ 处的函数值 $y_i=f(x_i)\quad(i=1,\cdots,n)$，简单函数类 S 的基函数 $\varphi_1(x),\varphi_2(x),\cdots,\varphi_n(x)$ 在 $[a,b]$ 上满足 Haar 条件，则存在唯一的 $p(x)=\sum\limits^n_{k=1}c_k\varphi_k(x)\in S$ 满足插值条件 $p(x_i)=y_i,\quad i=1,\cdots,n$

插值基函数：函数 $l_1(x),l_2(x),\cdots,l_n(x)$ 满足

$$l_k(x_i)=\delta_{i,k}= \left\{ \begin{array}{l} 1,i=k,\\0,i\neq k, \end{array} \right. \quad k=1,\cdots,n;\;i=1,\cdots,n$$

则 $l_k(x)(k=1,2,\cdots,n)$ 称为插值基函数

插值函数存在唯一性定理：在上述定理的假设下，函数 $p(x)=\sum\limits^n_{k=1}y_kl_k(x)$ 是 S 中满足插值条件 $p(x_i)=y_i,\;i=1,2,\cdots,n$ 的唯一函数。

5.2 多项式插值

Lagrange 插值和 Newton 插值的构造过程有区别，但最后得到的插值函数是一样的

Lagrange 插值

先给系数，再确定基底

系数为给定的函数值

假定构造的 n 次插值多项式为：

$$p(x)=y_0l_0(x)+y_1l_1(x)+\cdots+y_nl_n(x)$$

由插值条件 $p(x_i)=f(x_i)=y_i$ 知，基函数 $l_i(x)$ 需满足

$$l_i(x_k)= \left\{ \begin{array}{l} 1,\;k=i\\ 0,\;k\neq i \end{array} \right. \quad i,k=0,1,\cdots,n$$

$l_i(x),\;(i=0,1,\cdots,n)$ 称为 n 次 Lagrange 插值基函数.

Lagrange 插值基函数 为：

$$l_i(x)= \frac{(x-x_0)\cdots(x-x_{i-1})(x-x_{i+1})\cdots(x-x_n)} {(x_i-x_0)\cdots(x_i-x_{i-1})(x_i-x_{i+1})\cdots(x_i-x_n)} = \frac{w_{n+1}(x)} {(x-x_i)w'_{n+1}(x_i)}$$

其中

$$w_{n+1}(x)=(x-x_0)(x-x_1)\cdots(x-x_n)$$

多项式 $p_n(x)=\sum\limits^n_{i=1}y_il_i(x)$，就是多项式空间 $P_n(x)$ 中满足插值条件 $p_n(x_i)=y_i\quad (i=0,1,\cdots,n)$ 的唯一多项式，$p_n(x)$ 称为 n 次 Lagrange 插值多项式

注意：

• 插值基函数的个数 = 插值节点的个数
• 插值基函数的次数 = 插值节点的个数 - 1
• 插值基函数与插值节点的次序无关

并且，Lagrange 插值基函数具有如下性质：

• 设 $x_0,\cdots,x_n$ 是互异的插值节点组，$l_i(x)$ 是 Lagrange 插值基函数，则对于次数不超过 n 的多项式 $f(x)$，插值多项式 $p_n(x)=\sum\limits^n_{i=0}f(x_i)l_u(x)$ 精确成立，即 $p_n(x)=f(x)$，且 $p_n(x_0)=\sum\limits^n_{i=0}f(x_i)l_u(x_0)=f(x_0)$，特别的 ，$\sum\limits^n_{i=0}x^k_il_i(x)=x^k,\quad 0\leq k\leq n$。

• n+1 个节点的拉格朗日插值基函数之和为 1

• $$\sum_{i=0}^n\int_a^bl^2_i(x)dx= \sum_{i=0}^n\int_a^bl_i(x)dx= \int_a^b\sum_{i=0}^nl_i(x)dx=\int^b_a1dx=b-a$$

例题

Newton 插值

先给基底，再确定系数

克服了 Lagrange 插值难以灵活增加插值节点的缺点

设已知函数 $f(x)$ 在 $[a,b]$ 上的 $n+1$ 个互异插值节点 $x_0,x_1,\cdots,x_n$ 上的函数值 $f_0,f_1,\cdots,f_n$，将基函数取作：

$$\left\{ \begin{array}{l} \varphi_0(x)=1, \\ \varphi_j(x)=(x-x_0)(x-x_1)\cdots(x-x_{j-1})=\prod\limits^{j-1}_{i=0}(x-x_j),\; j=1,2,\cdots,n \end{array} \right.$$

则可将 n 次插值多项式写成如下形式

$$\begin{aligned} p_n(x)&=\sum\limits^n_{j=0}a_j\varphi_j(x) \\&=a_0+a_1(x-x_0)+\cdots+a_n(x-x_0)(x-x_1)\cdots(x-x_{n-1}) \end{aligned}$$

其中待定系数 $a_0,a_1,\cdots,a_n$ 由插值条件

$$p(x_i)=f_i,i=0,1,\;\dots,n$$

来确定；这些系数通过差商（均差）计算得到。

差商（均差）定义：设函数 $f(x)$ 在互异节点 $x_0,x_1,\cdots,x_n$ 上的函数值为 $f_0,f_1,\cdots,f_n$，称

$$f[x_i,x_k]=\frac{f_k-f_i}{x_k-x_i}\quad k\neq i$$

为 $f(x)$ 关于 $x_i,x_k$ 的一阶均差（差商），称

$$f[x_i,x_j,x_k]=\frac{f[x_j,x_k]-f[x_i,x_j]}{x_k-x_i}\quad i\neq j\neq k$$

为 $f(x)$ 关于 $x_i,x_j,x_k$ 的二阶均差（差商），称

$$f[x_0,x_1,\cdots,x_k]=\frac{f[x_1,\cdots,x_{k-1},x_k]-f[x_0,x_1,\cdots,x_{k-1}]}{x_k-x_0}$$

为 $f(x)$ 关于 $x_0,x_1,\cdots,x_k$ 的 k 阶均差（差商）.

运用均差表计算均差

例如，当 $f(0)=2,f(1)=-3,f(2)=-6,f(3)=11$ 时

则有

$$\begin{aligned} p_n(x)&=f(x_0)+f[x_0,x_1](x-x_0)+f[x_0,x_1,x_2](x-x_0)(x-x_1)\\ &\;\;\;\;\;+\cdots+f[x_0,x_1,\cdots,x_n](x-x_0)(x-x_1)\cdots(x-x_{n-1})\\ \end{aligned}$$

若

$$\lim_\limits{x_0=x_1=\cdots=x_k}f[x_0,x_1,\cdots,x_k]=\lim\limits_{\xi\to x_0}\frac{f^{(k)}(\xi)}{k!}=\frac{f^{(k)}(x_0)}{k!}$$

均差可以表示为 Taylor 多项式

均差的性质：

• k 阶均差计算公式：

  $$f[x_0,x_1,\cdots,x_k]=\sum\limits_{j=0}^k\frac{f(x_j)}{w'_{k+1}(x_j)}$$

  其中 $w_{k+1}(x)=(x-x_0)(x-x_1)\cdots(x-x_k)$

• 对称性，即在 $f[x_0,x_1,\cdots,x_k]$ 中任意调换 $x_0,x_1,\cdots,x_k$ 的位置时，均差的值不变

  $$f[x_0,x_1,\cdots,x_k]=f[x_1,x_0,\cdots,x_k]=\cdots=f[x_k,x_0,x_1,\cdots,x_{k-1}]$$

• 若 $f(x)=x^m$，m为自然数，则

  $$f[x_0,x_1,\cdots,x_k]= \left\{ \begin{array}{l} 0,\;k>m\\ 1,\;k=m\\ 诸 x_i 的 m-k 次齐次函数 ,k<m \end{array} \right.$$

• 设 $f(x)$ 在包含 $x_0,x_1,\cdots,x_k$ 的区间 $(a,b)$ 内 k 次可微，则

  $$f[x_0,x_1,\cdots,x_k]=\frac{f^{(k)}(\xi)}{k!}$$

  ，此处 $\min(x_0,x_1,\cdots,x_k)<\xi<\max(x_0,x_1,\cdots,x_k)$

Newton 插值多项式：n 次 Newton 插值多项式公式可以表示为：

$$\begin{aligned} p_n(x)&=f(x_0)+f[x_0,x_1](x-x_0)+f[x_0,x_1,x_2](x-x_0)(x-x_1)\\ &\;\;\;\;\;+\cdots+f[x_0,x_1,\cdots,x_n](x-x_0)(x-x_1)\cdots(x-x_{n-1})\\ &=p_{n-1}(x)+f[x_0,x_1,\cdots,x_n](x-x_0)(x-x_1)\cdots(x-x_{n-1}) \end{aligned}$$

插值多项式具有唯一性，Newton 插值多项式和 Lagrange 插值多项式的表现形式不同，最后可以化为相同的表达式

例题

插值余项

定义：若 $f(x)$ 在包含着插值节点 $x_0,x_1,\cdots,x_n$ 的区间 $[a,b]$ 上 n+1 次可微，则对任意 $x\in[a,b]$，存在与 x 有关的 $\xi\;(a<\xi<b)$，使得

$$r_n(x)=f(x)-p_n(x)=\frac{f^{(n+1)}(\xi)}{(n+1)!}w_{n+1}(x)$$

其中 $w_{k+1}(x)=(x-x_0)(x-x_1)\cdots(x-x_k)$

例题

Hermite 插值

要求插值函数具有一定的光滑度，在插值节点处满足一定的导数条件，这类插值问题称为 Hermite 问题

考试时，可通过待定系数法或均差表构造

设已知函数 f(x) 在 s 个互异点 $x_1,\cdots,x_s$ 处的函数值和导数值:

$$f(x_1),f'(x_1),\cdots,f^{(a_1-1)}(x_1);\\ f(x_2),f'(x_2),\cdots,f^{(a_2-1)}(x_2);\\ \cdots\cdots\\ f(x_s),f'(x_s),\cdots,f^{(a_s-1)}(x_s);\\$$

其中 $a_1,a_2,\cdots,a_s$ 为正整数，有 $a_1+a_2+\cdots+a_s=n+1$，构造一个 n 次多项式 $p_n(x)$，使其满足插值条件:

$$p_n^{(\mu_i)}(x_i)=f^{(\mu_i)}(x_i)=y_i^{(\mu_i)},\;i=1,2,\cdots,s;\;\mu_i=0,1,\cdots,a_i-1$$

可采用类似于构造 Largrange 插值基函数的方法解决 Hermite 插值问题，构造一批 n 次多项式 $L_{i,k}(x),i=1,2,\cdots,s;k=0,1,\cdots,a_i-1$，使这些多项式满足条件:

$$L_{i,k}^{(h)}(x_m)=0,m\neq i,h=0,1,\cdots,a_m-1;\\ L^{(h)}_{i,k}(x_i)= \left\{ \begin{array}{l} 0,h\neq k\\ 1,h=k \end{array} \right.$$

只要解决上述问题，则 n 次多项式

$$p_n(x)= \sum\limits^s_{i=1}\sum\limits^{a_i-1}_{k=0}y_i^{(k)}L_{i,k}(x)=\sum\limits^s_{i=1}[y_iL_{i,0}(x)+y_i^{(1)}L_{i,1}(x)+\cdots+y_i^{(a_i-1)}L_{i,a_i-1}(x)]$$

必满足插值条件

运用均差计算三次 Hermite 插值

则所求的三次插值多项式为：

$$H_3(x)=f(x_0)+f'(x_0)(x-x_0)+f[x_0,x_1,x_1](x-x_0)^2+f[x_0,x_0,x_1,x_1](x-x_0)^2(x-x_1)$$

例题

已知 $f(x)=a_0+a_1x+a_2x^2+a_3x^3$ 满足插值条件 $f(0)=1,f’(0)=2,f(1)=10,f’(1)=20$，求 $a_0,a_1,a_2,a_3$

解：这里可以通过两点三次的 Hermite 插值公式求得（此处例 3），也可以完全不需要利用公式，可以使用待定系数法求解如下方程，得到所需答案

$$f(x)=a_0+a_1x+a_2x^2+a_3x^3\\ f'(x)=a_1+2a_2x+3a_3x^2\\ f(0)=a_0=1\\ f(1)=a_0+a_1+a_2+a_3=10\\ f'(0)=a_1=2\\ f'(1)=a_1+2a_2+3a_3=20$$

1

2

3 两点三次的 Hermite 插值公式以及余项和误差估计

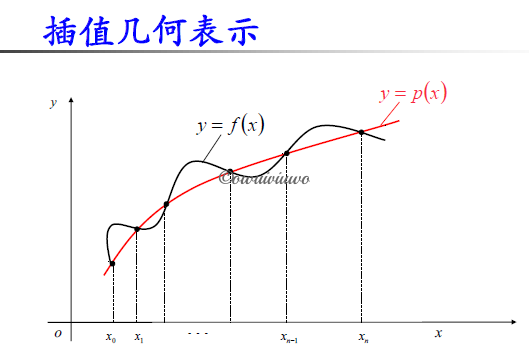
分段低次插值（应该不会考

插值节点越密集，插值函数的误差不一定越小，可能出现大幅的震荡。分段低次插值可避免高次插值可能出现的 Runge 现象

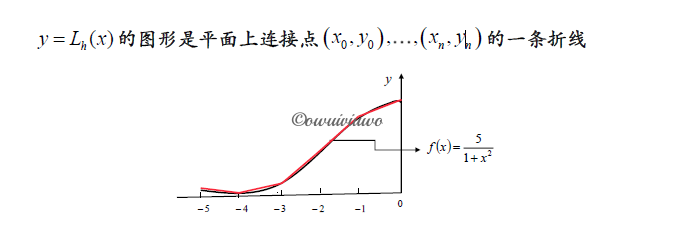
例题

5.3 三次样条插值（只考是样条函数的判定）

样条函数是满足一定光滑性的分段多项式，局部性好，满足一定光滑性，收敛性保证，只需函数值信息。

概念：对区间 $(-\infty,+\infty)$ 的一个分割：

$$\Delta:-\infty<x_1<x_2<\cdots<x_n<+\infty$$

若分段函数 $s(x)$ 满足条件

• 在每个区间 $(-\infty,x_1],x_j,x_j+1$ 和 $[x_n,+\infty)$ 上，$s(x)$ 是一个次数不超过 m 的实系数代数多项式
• $s(x)$ 在区间 $(-\infty,+\infty)$ 上具有直至 m-1 阶的连续微商，则称 y=s(x) 为对应于分割 $\Delta$ 的 m 次样条函数，$x_1,x_2,\cdots,x_n$ 为样条节点；以 为节点的 m 次样条函数的全体记为：$s_m(x_1,x_2,\cdots,x_n)$

样条函数判定定理

$$s(x)=\left\{ \begin{array}{l} p_0(x),\;x\leq x_1\\ p_1(x),x_1\leq x\leq x_2\\ \qquad\qquad\vdots\\ p_j(x),\;x_j\leq x\leq x_j+1\quad p_j(x)\in P_m(j)(j=0,1,\cdots,n)\\ \qquad\qquad\vdots\\ p_n(x),\; x_n\leq x \end{array} \right.$$

于是 s(x) 是 m 次样条的充要条件为：

$$p_0(x)=a_0+a_1x+\cdots+a_mx^m,\\ p_1(x)=p_0+c_1(x-x_1)^m,\\ p_2(x)=p_1(x)+c_2(x-x_2)^m=p_0+c_1(x-x_1)^m+c_2(x-x_2)^m\\ \cdots\\ p_n(x)=p_{n-1}+c_n(x-x_n)^m=p_0(x)+\sum\limits^n_{j=1}c_j(x-x_j)^m$$

其中，$c_i,\;i=1,\cdots,n$ 表示光滑因子，为常数

显然，针对三次样条函数的判定，m = 3

例题

*截断多项式

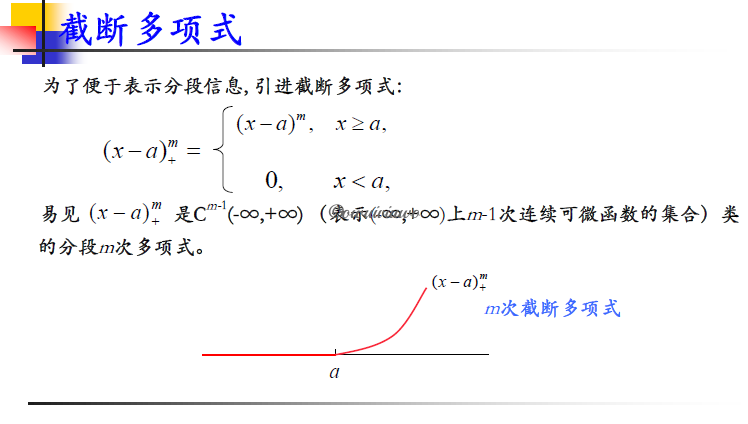
*三次样条插值构造及其收敛性

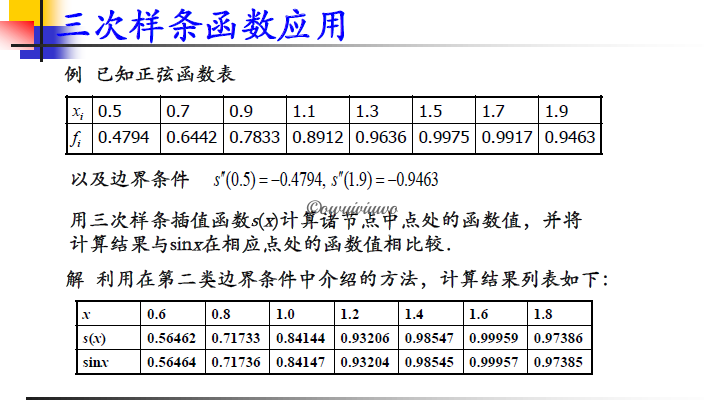
*三次样条函数的三种构造算法

1. 满足第一类边界条件（固定边界，Clamped Cubic Spline）

   p155-p156; algorithm 3.5; Numerical Analysis 9th Autor: Richard L.Burden and J.Douglas Faires

   

   

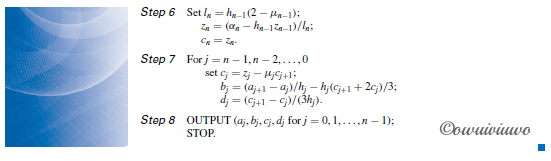
2. 满足第二类边界条件 （自然边界，Natural Cubic Spline）

   p149-p150; algorithm 3.4; Numerical Analysis 9th Autor: Richard L.Burden and J.Douglas Faires

   给出首尾两点的二阶导数值为 0，即 $S’’(x_0)=S’’(x_n)=0$

   

   

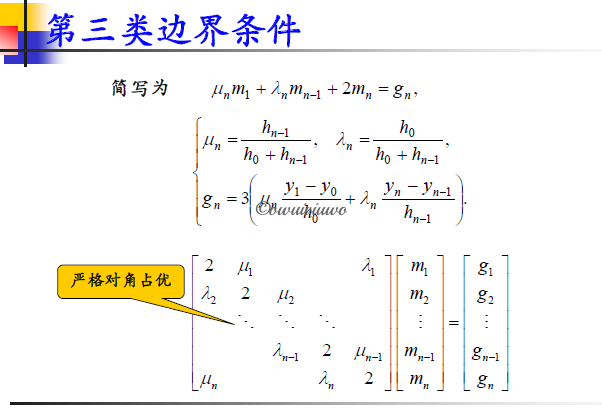
3. 满足第三类边界条件

   https://blog.csdn.net/BJMzheng/article/details/117017335

5.4 正交函数族应用

连续型函数内积

连续型内积：对于 $[a,b]$ 上的连续函数 $f(x),g(x)$，定义连续型内积：

$$(f,g)=\int_a^b\rho(x)f(x)g(x)dx$$

其中可积函数 $\rho(x)\geq0\;\;(x\in[a,b])$ 是权函数.

类似于向量内积，连续型函数内积具有如下性质：

• $$(f,f)\geq0,(f,f)=0\Leftrightarrow f\equiv0$$

• $$(f,g)=(g,f)$$
• $$(\lambda f,g)=\lambda\cdot(f,g)$$
• $$(f+g,h)=(f,h)+(g,h)$$

• $f(x)$ 和 $g(x)$ 在 $[a,b]$ 上关于权函数 $\rho(x)$ 正交，则 $(f,g)=0$

正交多项式系

正交多项式系：利用 Schmidt 正交化构造正交多项式，特别取多项式系 $1,x,\cdots,x^n,\cdots$ 进行正交化即得正交多项式系；令

$$\mu_m=\int_a^b=\rho(x)\cdot x^mdx,\;\;m=0,1,\cdots$$

取

$$\phi_0(x)=1,\phi_i(x)= \begin{vmatrix} \mu_0&\mu_1&\cdots&\mu_{i-1}&1\\ \mu_1&\mu_2&\cdots&\mu_{i}&x\\ \cdots&\cdots&\cdots&\cdots&\cdots\\ \mu_i&\mu_{i+1}&\cdots&\mu_{2i-1}&x^i\\ \end{vmatrix}$$

则 $\phi_0(x),\phi_i(x),\;i=1,2,\cdots$ 构成正交多项式系。

标准正交多项式系：令

$$\Delta= \begin{vmatrix} \mu_0&\mu_1&\cdots&\mu_i\\ \mu_1&\mu_2&\cdots&\mu_{i+1}\\ \vdots&\vdots&\ddots&\vdots\\ \mu_i&\mu_{i+1}&\cdots&\mu_{2i}\\ \end{vmatrix} ,\quad i=0,1,\cdots \\ \left\{ \begin{array}{l} \psi_0(x)=\frac{\phi_0(x)}{\sqrt{(\phi_0,\phi_0)}}=\frac{1}{\sqrt{\Delta_0}}\\ \psi_i(x)=\frac{\phi_i(x)}{\sqrt{(\phi_i,\phi_i)}}=\frac{\phi_i(x)}{\sqrt{\Delta_{i-1}\Delta_i}} \end{array} \right. ,\;i=0,1,\cdots$$

则 $\psi_0(x),\psi_1(x),\cdots,\psi_n(x)$ 成为标准正交多项式系。

正交多项式的一些性质：

1. $\phi_n(x)$ 恰好是 n 次多项式，$\phi_0(x),\phi_1(x),\cdots,\phi_n(x)$ 是 $P_n$ 的一组基底函数

2. $\phi_n(x)$ 与次数低于 n 次的所有多项式正交

3. $\phi_n(x)$ 在 $(a,b)$ 内恰有 n 个互异零点

4. 设 $p_k$ 为首项系数为 1 的 k 次正交多项式，则有如下三角递推关系式成立

   $$p_{k+1}=(x-\alpha_k)p_k-\beta_{k-1}p_{k-1}$$

   其中 $\alpha_k=\frac{(xp_k,p_k)}{(p_k,p_k)},\beta_k=\frac{(p_k,p_k)}{(p_{k-1},p_{k-1})}$

性质 2,3 是 C6 中构造 Gauss 型求积公式的重要依据

例子

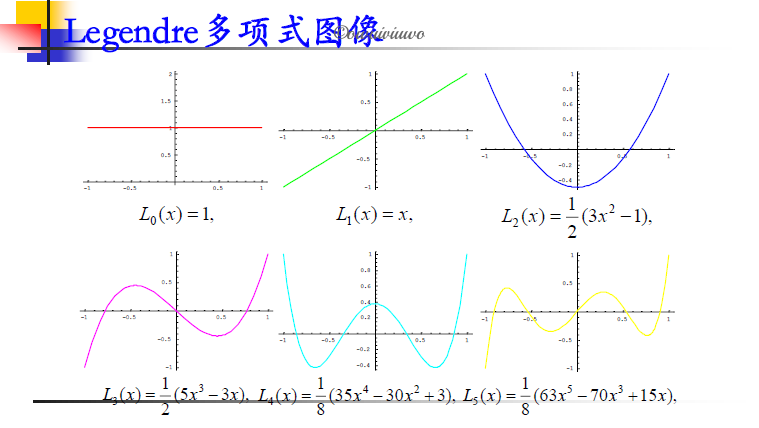
Legendre 多项式： 在 $[-1,1]$ 上以 $\rho(x)=1$ 为权函数的正交多项式系为 Legendre 多项式系

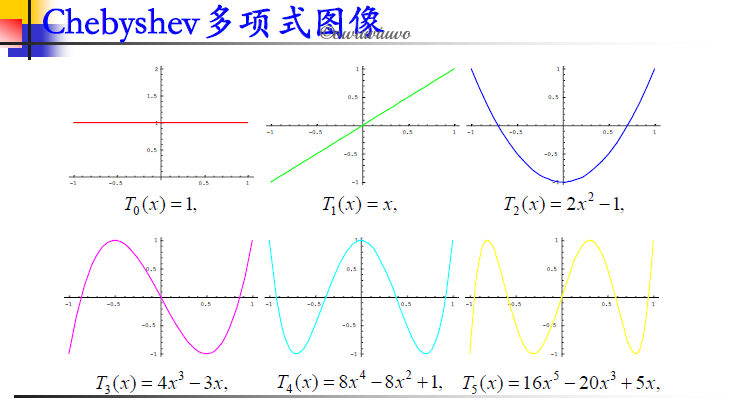
Chebyshev 多项式

1

数据拟合的最小二乘法

几何的意义

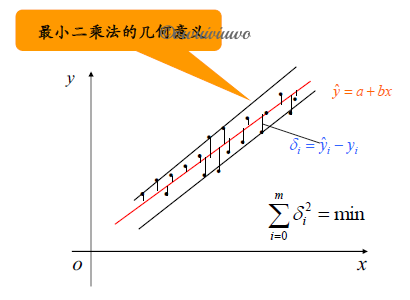
概念：设 $(x_i,y_i)(i=0,1,\cdots,m)$ 为给定的一组数据求一个函数

$$\hat{y}=a+bx$$

使其满足

$$\min=\sum\limits^m_{i=0}(\hat{y}(x_i)-y_i)^2$$

则称按上述条件求 $\hat{y}(x)$ 的方法为离散数据拟合 $\{x_i,y_i\}^m_{i=0}$ 的最小二乘法，简称最小二乘法，并称 $\hat{y}(x)$ 为最小二乘解

求解 $\hat{y}(x)$ 等价于求多元数

$$E(a,b)=\sum\limits^m_{i=0}(\hat{y}(x_i)-y_i)^2=\sum\limits^m_{i=0}((a+bx_i)-y_i)^2$$

的最小值点 $(a^,b^)$

最后可以写成矩阵形式，可通过所给点构造并求解法方程组

针对一次函数求解(注意这里 a 是常数，b 是一次项系数) $y=a+bx$ 的法方程组为

$$\begin{pmatrix} \sum\limits^m_{i=0}x_i^0=m+1&\sum\limits^m_{i=0}x_i\\ \sum\limits^m_{i=0}x_i&\sum\limits^m_{i=0}x_i^2 \end{pmatrix} \begin{pmatrix} a\\b \end{pmatrix} = \begin{pmatrix} \sum\limits^m_{i=0}y_i\\ \sum\limits^m_{i=0}x_i\cdot y_i \end{pmatrix}$$

类似的，针对二次函数求解 $y=a+bx+cx^2$ 的法方程组为

$$\begin{pmatrix} \sum\limits^m_{i=0}x_i^0=m+1&\sum\limits^m_{i=0}x_i&\sum\limits^m_{i=0}x_i^2\\ \sum\limits^m_{i=0}x_i&\sum\limits^m_{i=0}x_i^2&\sum\limits^m_{i=0}x_i^3\\ \sum\limits^m_{i=0}x_i^2&\sum\limits^m_{i=0}x_i^3&\sum\limits^m_{i=0}x_i^4 \end{pmatrix} \begin{pmatrix} a\\b\\c \end{pmatrix} = \begin{pmatrix} \sum\limits^m_{i=0}y_i\\ \sum\limits^m_{i=0}x_i\cdot y_i\\ \sum\limits^m_{i=0}x_i^2\cdot y_i \end{pmatrix}$$

更高次的构造方法也与之类似

推导过程如下

例题

正常考试题的流程为：依据所给数据，构造法方程组求解即可，可能会涉及到线性函数与非线性函数的转换，这一过程包括所给的数据与系数，例如

$$y=x^b\Rightarrow \ln y=\ln c + b\cdot\ln x\Rightarrow z=a+bt\qquad z=\ln y,t=\ln x,a=\ln c\\ y=ce^{bx}\Rightarrow \ln y=\ln c + b x\Rightarrow z=a+bt\qquad z=\ln y,a=\ln c\\ y=\frac{1}{a+bx}\Rightarrow \frac{1}{y}=a+bx\Rightarrow z=a+bx\qquad z=\frac{1}{y}\\ y=a+\frac{b}{x}\Rightarrow y=a+bt\qquad t=\frac{1}{x}$$

线性的情况

非线性的情况