C5 插值与逼近
5.1 引言

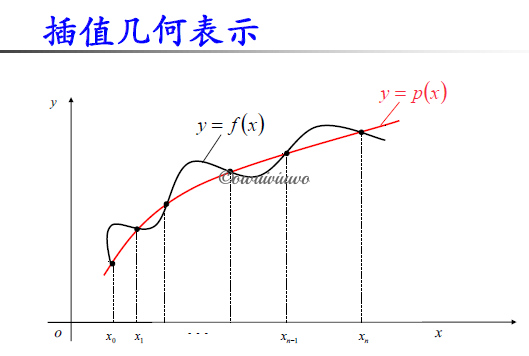

有 n 个插值节点,就有 n 插值条件,可以构造至多 n-1 次的插值函数
需要考虑简单函数类的选取问题: 如代数多项式, 三角多项式,分段多项式,有理函数,样条函数等;存在唯一性问题;余项估计问题;收敛性问题等
思想是:简单函数类的基底需满足条件;给出具体的基底;给出系数


解存在条件-Harr 条件:设 $\varphi_1(x),\varphi_2(x),\cdots,\varphi_n(x)$ 是 $[a,b]$ 上的函数,且对 上的任意 n 个互异点 $x_1,x_2,\cdots,x_n$,有行列式
则称 $\varphi_1(x),\varphi_2(x),\cdots,\varphi_n(x)$ 在 $[a,b]$ 上满足 Haar 条件
解存在唯一性定理:设已知函数 $f(x)$ 在 n 个互异点 $x_1,x_2,\cdots,x_n$ 处的函数值 $y_i=f(x_i)\quad(i=1,\cdots,n)$,简单函数类 S 的基函数 $\varphi_1(x),\varphi_2(x),\cdots,\varphi_n(x)$ 在 $[a,b]$ 上满足 Haar 条件,则存在唯一的 $p(x)=\sum\limits^n_{k=1}c_k\varphi_k(x)\in S$ 满足插值条件 $p(x_i)=y_i,\quad i=1,\cdots,n$
插值基函数:函数 $l_1(x),l_2(x),\cdots,l_n(x)$ 满足
则 $l_k(x)(k=1,2,\cdots,n)$ 称为插值基函数
插值函数存在唯一性定理:在上述定理的假设下,函数 $p(x)=\sum\limits^n_{k=1}y_kl_k(x)$ 是 S 中满足插值条件 $p(x_i)=y_i,\;i=1,2,\cdots,n$ 的唯一函数。
5.2 多项式插值
Lagrange 插值和 Newton 插值的构造过程有区别,但最后得到的插值函数是一样的
Lagrange 插值
先给系数,再确定基底
系数为给定的函数值
假定构造的 n 次插值多项式为:
由插值条件 $p(x_i)=f(x_i)=y_i$ 知,基函数 $l_i(x)$ 需满足
$l_i(x),\;(i=0,1,\cdots,n)$ 称为 n 次 Lagrange 插值基函数.
Lagrange 插值基函数 为:
其中
多项式 $p_n(x)=\sum\limits^n_{i=1}y_il_i(x)$,就是多项式空间 $P_n(x)$ 中满足插值条件 $p_n(x_i)=y_i\quad (i=0,1,\cdots,n)$ 的唯一多项式,$p_n(x)$ 称为 n 次 Lagrange 插值多项式
注意:
- 插值基函数的个数 = 插值节点的个数
- 插值基函数的次数 = 插值节点的个数 - 1
- 插值基函数与插值节点的次序无关
并且,Lagrange 插值基函数具有如下性质:
设 $x_0,\cdots,x_n$ 是互异的插值节点组,$l_i(x)$ 是 Lagrange 插值基函数,则对于次数不超过 n 的多项式 $f(x)$,插值多项式 $p_n(x)=\sum\limits^n_{i=0}f(x_i)l_u(x)$ 精确成立,即 $p_n(x)=f(x)$,且 $p_n(x_0)=\sum\limits^n_{i=0}f(x_i)l_u(x_0)=f(x_0)$,特别的 ,$\sum\limits^n_{i=0}x^k_il_i(x)=x^k,\quad 0\leq k\leq n$。
n+1 个节点的拉格朗日插值基函数之和为 1
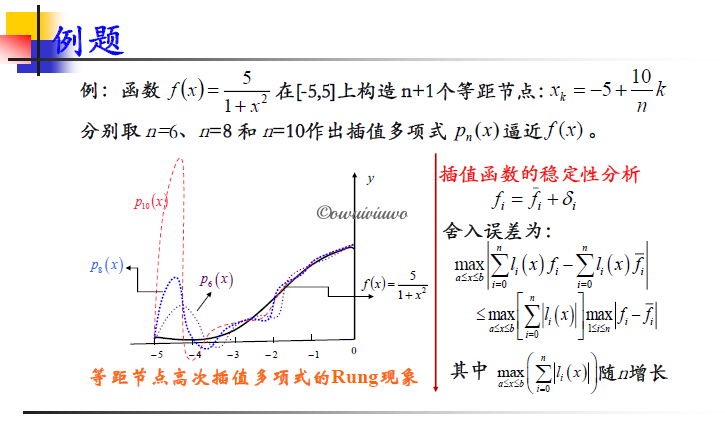
例题

Newton 插值
先给基底,再确定系数
克服了 Lagrange 插值难以灵活增加插值节点的缺点
设已知函数 $f(x)$ 在 $[a,b]$ 上的 $n+1$ 个互异插值节点 $x_0,x_1,\cdots,x_n$ 上的函数值 $f_0,f_1,\cdots,f_n$,将基函数取作:
则可将 n 次插值多项式写成如下形式
其中待定系数 $a_0,a_1,\cdots,a_n$ 由插值条件
来确定;这些系数通过差商(均差)计算得到。
差商(均差)定义:设函数 $f(x)$ 在互异节点 $x_0,x_1,\cdots,x_n$ 上的函数值为 $f_0,f_1,\cdots,f_n$,称
为 $f(x)$ 关于 $x_i,x_k$ 的一阶均差(差商),称
为 $f(x)$ 关于 $x_i,x_j,x_k$ 的二阶均差(差商),称
为 $f(x)$ 关于 $x_0,x_1,\cdots,x_k$ 的 k 阶均差(差商).
运用均差表计算均差
| x | f(x) | 一阶均差(1) | 二阶均差(2) | 三阶均差(3)$\cdots$ |
|---|---|---|---|---|
| $x_0$ | $f(x_0)$ | |||
| $x_1$ | $f(x_1)$ | $f[x_0,x_1]$ | ||
| $x_2$ | $f(x_2)$ | $f[x_1,x_2]$ | $f[x_0,x_1,x_2]$ | |
| $x_3$ | $f(x_3)$ | $f[x_2,x_3]$ | $f[x_1,x_2,x_3]$ | $f[x_0,x_1,x_2,x_3]$ |
例如,当 $f(0)=2,f(1)=-3,f(2)=-6,f(3)=11$ 时
| x | f(x) | 一阶均差(1) | 二阶均差(2) | 三阶均差(3)$\cdots$ |
|---|---|---|---|---|
| $0$ | $2$ | |||
| $1$ | $-3$ | $\frac{-3-2}{1-0}=-5$ | ||
| $2$ | $-6$ | $\frac{-6+3}{2-1}=-3$ | $\frac{-3+5}{2-0}=1$ | |
| $3$ | $11$ | $\frac{11+6}{3-2}=17$ | $\frac{17+3}{3-1}=10$ | $\frac{10-1}{3-0}=3$ |
则有
若
均差可以表示为 Taylor 多项式
均差的性质:
k 阶均差计算公式:
其中 $w_{k+1}(x)=(x-x_0)(x-x_1)\cdots(x-x_k)$
对称性,即在 $f[x_0,x_1,\cdots,x_k]$ 中任意调换 $x_0,x_1,\cdots,x_k$ 的位置时,均差的值不变
若 $f(x)=x^m$,m为自然数,则
设 $f(x)$ 在包含 $x_0,x_1,\cdots,x_k$ 的区间 $(a,b)$ 内 k 次可微,则
,此处 $\min(x_0,x_1,\cdots,x_k)<\xi<\max(x_0,x_1,\cdots,x_k)$
Newton 插值多项式:n 次 Newton 插值多项式公式可以表示为:
插值多项式具有唯一性,Newton 插值多项式和 Lagrange 插值多项式的表现形式不同,最后可以化为相同的表达式
例题




插值余项
定义:若 $f(x)$ 在包含着插值节点 $x_0,x_1,\cdots,x_n$ 的区间 $[a,b]$ 上 n+1 次可微,则对任意 $x\in[a,b]$,存在与 x 有关的 $\xi\;(a<\xi<b)$,使得
其中 $w_{k+1}(x)=(x-x_0)(x-x_1)\cdots(x-x_k)$
例题

Hermite 插值
要求插值函数具有一定的光滑度,在插值节点处满足一定的导数条件,这类插值问题称为 Hermite 问题
考试时,可通过待定系数法或均差表构造
设已知函数 f(x) 在 s 个互异点 $x_1,\cdots,x_s$ 处的函数值和导数值:
其中 $a_1,a_2,\cdots,a_s$ 为正整数,有 $a_1+a_2+\cdots+a_s=n+1$,构造一个 n 次多项式 $p_n(x)$,使其满足插值条件:
可采用类似于构造 Largrange 插值基函数的方法解决 Hermite 插值问题,构造一批 n 次多项式 $L_{i,k}(x),i=1,2,\cdots,s;k=0,1,\cdots,a_i-1$,使这些多项式满足条件:
只要解决上述问题,则 n 次多项式
必满足插值条件
运用均差计算三次 Hermite 插值
| x | f(x) | 一阶均差(1) | 二阶均差(2) | 三阶均差(3)$\cdots$ |
|---|---|---|---|---|
| $x_0$ | $f(x_0)$ | |||
| $x_0$ | $f(x_0)$ | $f[x_0,x_0]=f’(x_0)$ | ||
| $x_1$ | $f(x_1)$ | $f[x_0,x_1]$ | $f[x_0,x_0,x_1]$ | |
| $x_1$ | $f(x_1)$ | $f[x_1,x_1]=f’(x_1)$ | $f[x_0,x_1,x_1]$ | $f[x_0,x_0,x_1,x_1]$ |
则所求的三次插值多项式为:
例题
已知 $f(x)=a_0+a_1x+a_2x^2+a_3x^3$ 满足插值条件 $f(0)=1,f’(0)=2,f(1)=10,f’(1)=20$,求 $a_0,a_1,a_2,a_3$
解:这里可以通过两点三次的 Hermite 插值公式求得(此处例 3),也可以完全不需要利用公式,可以使用待定系数法求解如下方程,得到所需答案
1

2

3 两点三次的 Hermite 插值公式以及余项和误差估计


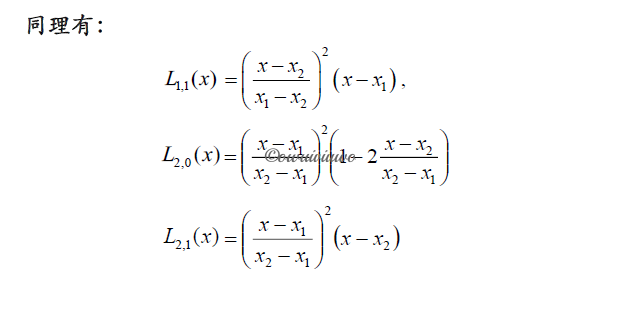

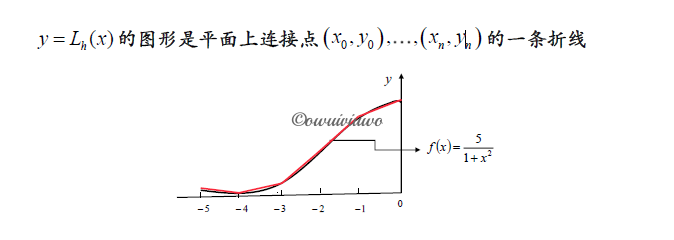
分段低次插值(应该不会考
插值节点越密集,插值函数的误差不一定越小,可能出现大幅的震荡。分段低次插值可避免高次插值可能出现的 Runge 现象




例题
5.3 三次样条插值(只考是样条函数的判定)
样条函数是满足一定光滑性的分段多项式,局部性好,满足一定光滑性,收敛性保证,只需函数值信息。
概念:对区间 $(-\infty,+\infty)$ 的一个分割:
若分段函数 $s(x)$ 满足条件
- 在每个区间 $(-\infty,x_1],x_j,x_j+1$ 和 $[x_n,+\infty)$ 上,$s(x)$ 是一个次数不超过 m 的实系数代数多项式
- $s(x)$ 在区间 $(-\infty,+\infty)$ 上具有直至 m-1 阶的连续微商,则称 y=s(x) 为对应于分割 $\Delta$ 的 m 次样条函数,$x_1,x_2,\cdots,x_n$ 为样条节点;以 为节点的 m 次样条函数的全体记为:$s_m(x_1,x_2,\cdots,x_n)$
样条函数判定定理
于是 s(x) 是 m 次样条的充要条件为:
其中,$c_i,\;i=1,\cdots,n$ 表示光滑因子,为常数
显然,针对三次样条函数的判定,m = 3
例题

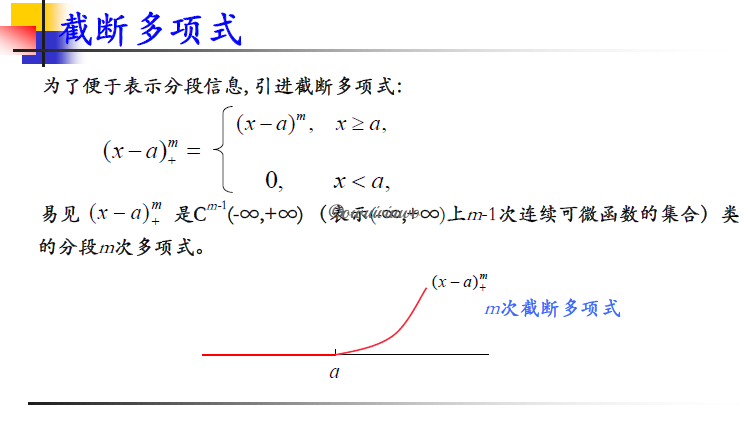
*截断多项式

*三次样条插值构造及其收敛性








*三次样条函数的三种构造算法
满足第一类边界条件(固定边界,Clamped Cubic Spline)
p155-p156; algorithm 3.5; Numerical Analysis 9th Autor: Richard L.Burden and J.Douglas Faires

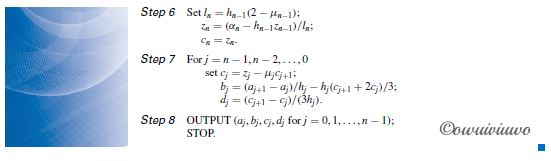
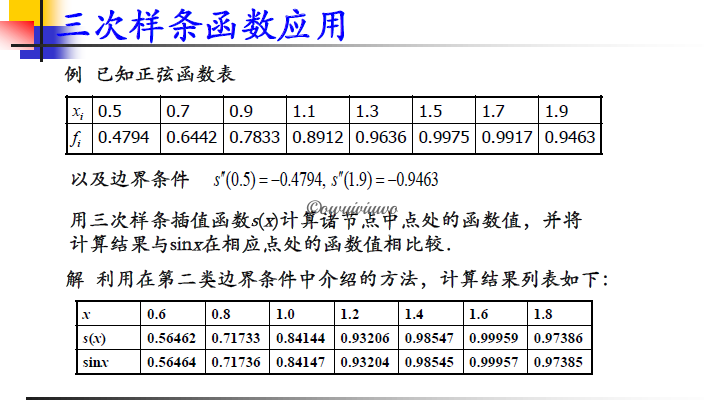
满足第二类边界条件 (自然边界,Natural Cubic Spline)
p149-p150; algorithm 3.4; Numerical Analysis 9th Autor: Richard L.Burden and J.Douglas Faires
给出首尾两点的二阶导数值为 0,即 $S’’(x_0)=S’’(x_n)=0$


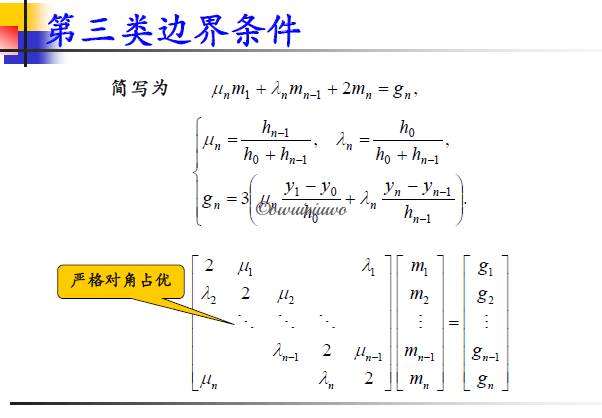
满足第三类边界条件
5.4 正交函数族应用
连续型函数内积
连续型内积:对于 $[a,b]$ 上的连续函数 $f(x),g(x)$,定义连续型内积:
其中可积函数 $\rho(x)\geq0\;\;(x\in[a,b])$ 是权函数.
类似于向量内积,连续型函数内积具有如下性质:
$f(x)$ 和 $g(x)$ 在 $[a,b]$ 上关于权函数 $\rho(x)$ 正交,则 $(f,g)=0$
正交多项式系
正交多项式系:利用 Schmidt 正交化构造正交多项式,特别取多项式系 $1,x,\cdots,x^n,\cdots$ 进行正交化即得正交多项式系;令
取
则 $\phi_0(x),\phi_i(x),\;i=1,2,\cdots$ 构成正交多项式系。
标准正交多项式系:令
则 $\psi_0(x),\psi_1(x),\cdots,\psi_n(x)$ 成为标准正交多项式系。
正交多项式的一些性质:
$\phi_n(x)$ 恰好是 n 次多项式,$\phi_0(x),\phi_1(x),\cdots,\phi_n(x)$ 是 $P_n$ 的一组基底函数
$\phi_n(x)$ 与次数低于 n 次的所有多项式正交
$\phi_n(x)$ 在 $(a,b)$ 内恰有 n 个互异零点
设 $p_k$ 为首项系数为 1 的 k 次正交多项式,则有如下三角递推关系式成立
其中 $\alpha_k=\frac{(xp_k,p_k)}{(p_k,p_k)},\beta_k=\frac{(p_k,p_k)}{(p_{k-1},p_{k-1})}$
性质 2,3 是 C6 中构造 Gauss 型求积公式的重要依据
例子
Legendre 多项式: 在 $[-1,1]$ 上以 $\rho(x)=1$ 为权函数的正交多项式系为 Legendre 多项式系

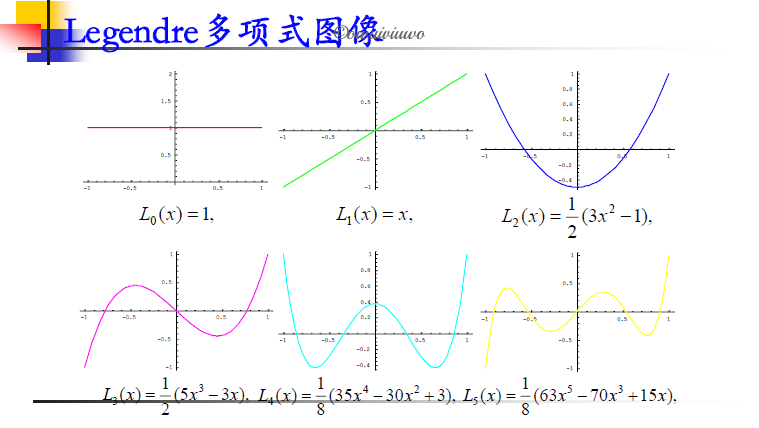

Chebyshev 多项式

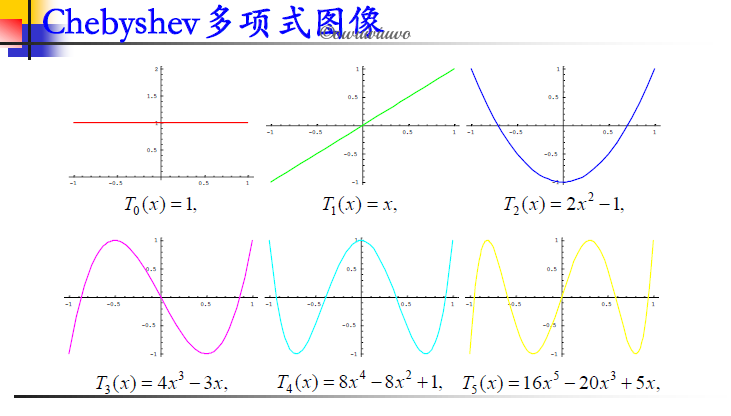

1

数据拟合的最小二乘法
几何的意义
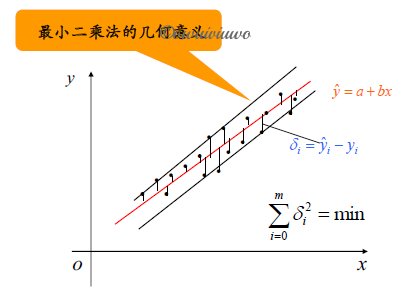
概念:设 $(x_i,y_i)(i=0,1,\cdots,m)$ 为给定的一组数据求一个函数
使其满足
则称按上述条件求 $\hat{y}(x)$ 的方法为离散数据拟合 $\{x_i,y_i\}^m_{i=0}$ 的最小二乘法,简称最小二乘法,并称 $\hat{y}(x)$ 为最小二乘解
求解 $\hat{y}(x)$ 等价于求多元数
的最小值点 $(a^,b^)$
最后可以写成矩阵形式,可通过所给点构造并求解法方程组
针对一次函数求解(注意这里 a 是常数,b 是一次项系数) $y=a+bx$ 的法方程组为
类似的,针对二次函数求解 $y=a+bx+cx^2$ 的法方程组为
更高次的构造方法也与之类似
推导过程如下




例题
正常考试题的流程为:依据所给数据,构造法方程组求解即可,可能会涉及到线性函数与非线性函数的转换,这一过程包括所给的数据与系数,例如
线性的情况


非线性的情况