2022-2023 春学期 矩阵与数值分析 C4 逐次逼近法

C4 逐次逼近法

4.1 解线性方程组的迭代法

简单迭代法迭代格式

可将线性方程组变形

$$Ax=b \Leftrightarrow x=Bx+f$$

其中 B 为迭代矩阵，且

$$B\in R^{n\times n},f\in R^n,x\in R^n$$

迭代法：称使用

$$x^{(k+1)}=Bx^{k}+f\;(k=0,1,2,\cdots)$$

求解的方法为迭代法，也称迭代过程或迭代格式.

迭代法收敛、发散：如果对任意 $x^{(0)}$ ，都有 $\lim\limits_{k\to\infty}x^{(k)}=x^*$。即

$$\lim\limits_{k\to\infty}x_i^{(k)}=x_i^*,\;i=1,2,\cdots,n$$

称该迭代法收敛，否则称迭代法发散。

Jacobi，Gauss-seidel 迭代法等

简单迭代法-方程组变形

线性方程组：

$$\left\{ \begin{array}{c} a_{11}x_1+a_{12}x_2+\cdots+a_{1n}x_n=b_1\\ \vdots\\ a_{n1}x_1+a_{n2}x_2+\cdots+a_{nn}x_n=b_n \end{array} \right.$$

等价方程组：$a_{ii}\neq0$

$$\left\{ \begin{array}{l} x_1=\frac{1}{a_{11}}(b_1-a_{12}x_2-\cdots-a_{1n}x_n)\\ \qquad\qquad\qquad\qquad\qquad\vdots\\ x_i=\frac{1}{a_{ii}}(b_i-a_{i1}x_1-\cdots-a_{ii-1}x_{i-1}-a_{ii+1}x_{i+1}-\cdots-a_{in}x_n)\\ \qquad\qquad\qquad\qquad\qquad\vdots\\ x_n=\frac{1}{a_{nn}}(b_a-a_{n1}x_1-\cdots-a_{nn-1}x_{n-1}) \end{array} \right.$$

Jacobi 迭代法：

$$x_i^{(k+1)}=\frac{1}{a_{ii}}(b_i-\sum\limits^{i-1}_{j=1}a_{ij}x_j^{(k)}-\sum\limits^n_{j=i+1}a_{ij}x_j^{(k)})\;(i=1,2,\cdots,n)$$

在 Jacobi 迭代过程中，对已经算出来的信息未加以充分利用，比如在计算 $x^{k+1}_2$ 时 $x^{k+1}_1$ 已经算出，可是使用 Seidel 技巧加以改进，得到 Gauss-Seidel 迭代法：

$$x_i^{(k+1)}=\frac{1}{a_{ii}}(b_i-\sum\limits^{i-1}_{j=1}a_{ij}x_j^{(k+1)}-\sum\limits^n_{j=i+1}a_{ij}x_j^{(k)})\;(i=1,2,\cdots,n)$$

矩阵分裂：可以将系数矩阵 A 分裂为 A=D-L-U 的形式，具体如下所示：

$$A=D-L-U\\$$ $$A= \begin{pmatrix} a_{1,1}&a_{1,2}&\cdots&a_{i,j}&\cdots&a_{1,n}\\ a_{2,1}&a_{2,2}&\cdots&\cdots&\cdots&a_{2,n}\\ \vdots&\ddots&\ddots&\vdots&\vdots&\vdots \\ a_{i,1}&\cdots&a_{i,j-1}&a_{i,j}&\cdots&a_{i,n} \\ \vdots&&\vdots&\ddots&\ddots&\vdots \\ a_{n,1}&\cdots&a_{n,j-1}&\cdots&a_{n,n-1}&a_{n,n} \end{pmatrix}\\$$ $$D=\mathrm{diag(a_{1,1},a_{2,2},\cdots,a_{n,n})}\\$$ $$L= \begin{pmatrix} 0&&&&&0\\ -a_{2,1}&0\\ \vdots&\ddots&\ddots\\ -a_{j,1}&\cdots&-a_{j,j-1}&0\\ \vdots&&\vdots&\ddots&\ddots\\ -a_{n,1}&\cdots&-a_{n,j-1}&\cdots&-a_{n,n-1}&0 \end{pmatrix}\\$$ $$U= \begin{pmatrix} 0&-a_{1,2}&\cdots&-a_{1,j}&\cdots&-a_{1,n}\\ &\ddots&\ddots&\vdots&&\vdots\\ &&0&-a_{j-1,j}&\cdots&-a_{j-1,n}\\ &&&\ddots&\ddots&\vdots\\ &&&&0&-a_{n-1,n}\\ 0&&&&&0\\ \end{pmatrix}\\$$

Jacobi、Gauss-Seidel 迭代法矩阵格式

由 A=D-L-U，得 Dx=(L+U)x+b 从而有：

$$x=D^{-1}(L+U)x+D^{-1}b$$

则 Jacobi 迭代法可写成：

$$x^{(k+1)}=D^{-1}(L+U)x^{(k)}+D^{-1}b;\;k=0,1,2,\cdots$$

由 A=D-L-U，得 (D-L)x=Ux+b 从而

$$x=(D-L)^{-1}Ux+(D-L)^{-1}b$$

则 Gauss-Seidel 迭代法可以写成：

$$x^{(k+1)}=(D-L)^{-1}Ux^{(k)}+(D-L)^{-1}b;\;k=0,1,2,\cdots$$

并不是对任何情况，G-S 迭代都比 Jacobi 迭代收敛速度快

例题

1

*迭代改善法（应该不会考）

迭代法的收敛性

迭代法收敛性定理（谱半径）：迭代法 $x^{(k+1)}=Bx^{(k)}+f$ 对任意 $x^{(0)}$ 和 $f$ 均收敛的充要条件为：

$$\rho(B)<1$$

迭代法收敛性定理（范数）：若迭代矩阵任意范数 $||B||<1$，则迭代法收敛，且有

$$||x^{(k)}-x^*||\leq\frac{||B||^k}{1-||B||}||x^{(1)}-x^{(0)}||$$

定理： $\lim\limits_{k\to\infty}\epsilon^{(k)}=0$（即迭代收敛 $x_i^{(k)}\to x_i^*,i=1,2,\cdots,n$）的充分必要条件是 $\lim\limits_{k\to\infty}B^k=0_{n\times n}\Leftrightarrow \rho(B)<1$

迭代法收敛性-特殊线性方程组

针对某些特殊方程组，从方程组本身就可以判定其收敛性，不必求迭代矩阵的特征值或范数

• 严格（不可约）对角占优矩阵

  • 定义：如果矩阵 $A=(a_{ij})_{n\times n}$ 的元素满足不等式 $|a_{ii}|\geq\sum\limits_{j=1,j!=i}^n|a_{ij}|,\;(i=1,2,\cdots,n)$，则称 A 为对角占优阵；如果所有严格不等式（即不等式不取等号）均成立，称 A 为严格对角占优矩阵。

  • 定理：严格对角占优阵 A 为非奇异矩阵，即 $\det(A)\neq0$

  • 定理：若线性方程组 Ax=b 中的 A 为严格对角占优矩阵，则 Jacobi 法和 Gauss-Seidel 法均收敛。

• 对称正定矩阵

  若 A 为对称正定矩阵：

  • 若 2D-A 为正定矩阵，则 Jacobi 迭代法收敛
  • Gauss-Seidel 迭代法收敛

例题

4.2 非线性方程迭代解法

相关的概念

根、零点：对于非线性方程 f(x)=0 ，若数 a 满足 f(a)=0，则称 a 为方程的根，或称函数 f(x) 的零点

有根区间：如果 f(x)=0 在区间 [a,b] 上仅有一个根，则称 [a,b] 为方程的单根区间；若方程在 [a,b] 上有多个根，则称 [a,b] 为方程的多根区间。方程的单根区间和多根区间统称为方程的有根区间；这里主要研究方程在单根区间上的求解方法。

将方程 f(x)=0 化为一个与它同解的方程 $x=\varphi(x)$，其中 $\varphi(x)$ 为 x 的连续函数；就代入初值可以进行迭代求解

简单迭代法：称 $x_{k+1}=\varphi(x)$ 为求解非线性方程的简单迭代法，也称迭代法或迭代过程或迭代格，$\varphi(x)$ 称为迭代函数，$x_k$ 称第 k 步的迭代之或简称迭代值。

迭代法收敛：如果由迭代格式缠身的数列收敛，即 $\lim\limits_{k\to\infty}x_k=a$，则称迭代法收敛，否则称迭代法发散；若迭代法收敛于 a，则有 $a=\varphi(a)\Leftrightarrow f(a)\equiv a$，则 a 就是方程的根。

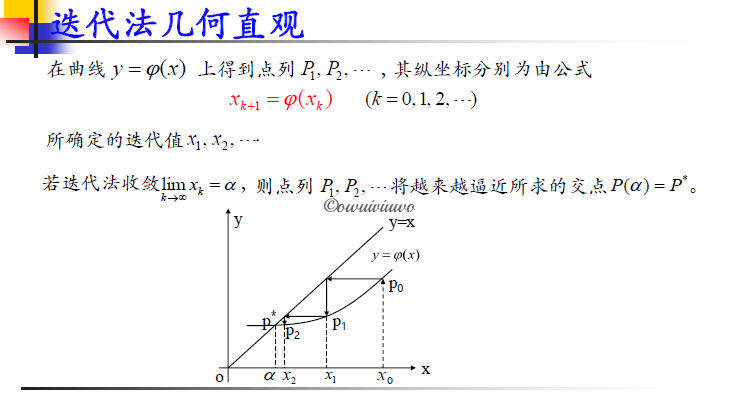
迭代法收敛

几何表示

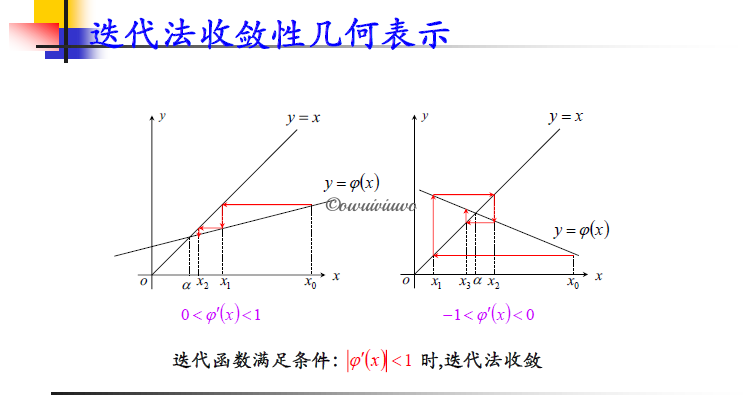
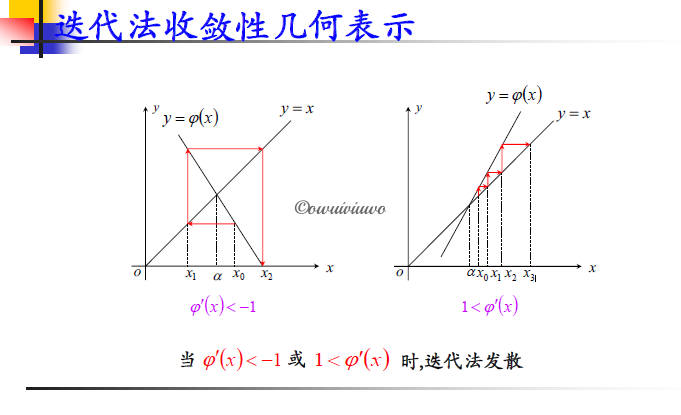
收敛性定理：设迭代函数 $\varphi(x)$ 满足

1. 当 $x\in[a,b]$ 时，$a\leq\varphi(x)\leq b$
2. 存在正数 $0<L<1$，对任意 $x\in[a,b]$ 均有 $|\varphi’(x)|\leq L$（难以验证）

则 $x=\varphi(x)$ 在 $[a,b]$ 内存在唯一根 $a$，且对任意初始值 $x_0\in[a,b]$ ，迭代法

$$x_{k+1}=\varphi(x_k)\;(k=0,1,2,\cdots)$$

收敛于 $a$，且

$$|x_k-a|\leq\frac{L}{1-L}|x_k-x_{k-1}|\leq\frac{L^k}{1-L}|x_1-x_0|$$

L 较小，相邻两次计算值的偏差 $|x_k-x_{k-1}|\leq\delta$ （事先给定的精度），迭代过程就可以终止，$x_k$ 就可以作为 a 的近似值

L 的大小可作出估计时，估计所需要的迭代次数

$$|x_k-a|\leq\frac{L^k}{1-L}|x_1-x_0|<\delta\rightarrow k\geq \log_L\frac{\delta(1-L)}{|x_1-x_0|}$$

使用迭代法时往往在根 a 的附近进行，假定 $\varphi’(x)$ 在 a 的附近连续且满足 $|\varphi’(a)|<1$，则一定存在 a 的某个领域 $S:|x-a|\leq\delta$ ，$\varphi(x)$ 在 S 上满足收敛性定理中的条件，所以在 S 中任取初始值 $x_0$，迭代格式

$$x_k=\varphi(x_{k-1})$$

收敛于方程的根 a，即 $f(a)\equiv0$，称此收敛为局部收敛。

误差估计式：

$$|x_k-a|\leq\frac{L^k}{1-L}|x_1-x_0|$$

中 L 或 $|\varphi’(x)|$ 在 $[a,b]$ 上的值越小，迭代的收敛速度就越快。L < 1 且接近于 1 时，迭代法虽然收敛，但收敛速度很慢。

为了使收敛速度有定量的判断， 特介绍收敛速度的阶的概念，作为判断迭代法收敛速度的重要标准。

设迭代格式 $x_{k+1}=\varphi(x_k)$，当 $k\to\infty$ 时，$x_{k+1}\to a$ 记 $e_k=x_k-a$

迭代法收敛阶：若存在实数 $p\geq1$ 和 $c>1$ 满足

$$\lim\limits_{k\to\infty}\frac{|e_{k+1}|}{|e_k|^p}=c$$

则称迭代法是 p 阶收敛，当 p=1 时，称线性收敛，当 p>1 时称超线性收敛，当 p=2 时称平方收敛。

显然：

• 收敛阶越大迭代法的收敛速度也越快
• 收敛阶难以直接确定，课采用一些其他方法来确定收敛阶（Taylor 展开式）

收敛阶判定定理

p 阶收敛：如果 $x=\varphi(x)$ 中的迭代函数 $\varphi(x)$ 在根 a 附近满足：

1. $\varphi(x)$ 存在 p 阶导数且连续

2. $$\varphi'(a)=\varphi''(a)=\cdots=\varphi^{(p-1)}(a)=0,\;\varphi^{(p)}(a)\neq0$$

   则迭代法 $x_{k+1}=\varphi(x_k)$ 是 p 阶收敛的

例题

1

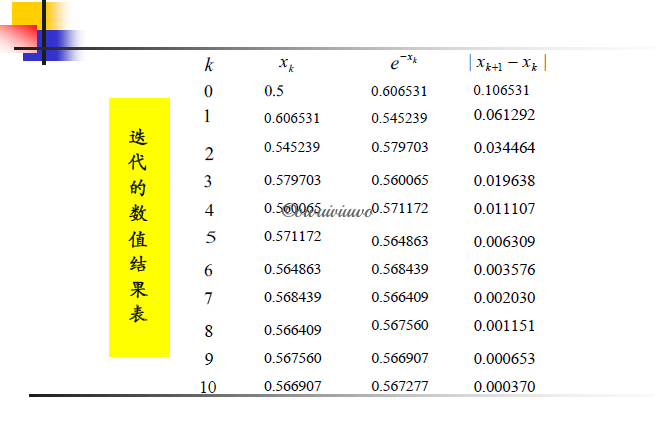
2

牛顿（Newton）法：

Newton 迭代法

Newton 迭代格式：设方程 $f(x)=0$ 的根为 $a$，且 $f’(a)\neq0$，则迭代法

$$x_{k+1}=x_k-\frac{f(x_k)}{f'(x_k)}\;(k=0,1,2,\cdots)$$

至少是平方收敛，并称该迭代格式为 Newton 迭代法。

类似的，可以使用导数的近似式 $f’(x)\approx\frac{f(x_k)-f(x_{k-1})}{x_k-x_{k-1}}$ 替代 $f’(x)$，可将其代入 Newton 迭代格式，得到割线法（弦截法）。

$$x_{k+1}=x_k-\frac{(x_k-x_{k-1})f(x_k)}{f(x_k)-f(x_{k-1})}$$

割线法是超线性收敛的（$p=\frac{1+\sqrt{5}}{2}\approx1.618$），低于 Newton 法

此外，还有单步弦截法

$$x_{k+1}=x_k-\frac{(x_k-x_{0})f(x_k)}{f(x_k)-f(x_{0})}$$

平行线法

$$x_{k+1}=x_k-\frac{f(x_k)}{f'(x_0)}$$

例题

1

2

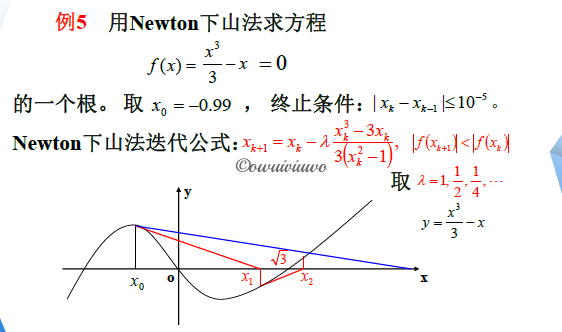
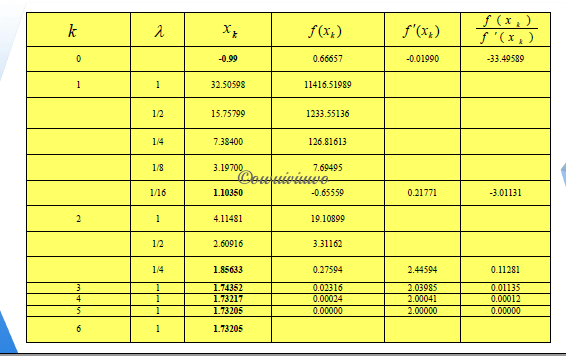
针对重根改进的 Newton 法：

设 $a$ 是 $f(x)=0$ 的 $m$ 重根（满足 $f(a)=f’(a)=f’’(a)=\cdots=f^{(m-1)}(a)=0,\;f^{(m)}\neq0$ ），其中 $m\geq2$ 是整数，则有 $f(x)=(x-a)^mg(x)$，且 $g(a)\neq0$

此时，直接使用 Newton 法是线性收敛而不是平方收敛的

$$\varphi(x)=x-\frac{f(x)}{f'(x)}=x-\frac{(x-a)^mg(x)}{m(x-a)^{(m-1)}g(x)+(x-a)^mg'(x)}$$ $$\varphi'(x)=1-\frac{g(x)}{mg(x)+(x-a)g'(x)}-(x-a) [\frac{g(x)}{m\cdot g(x)+(x-a)g'(x)}]'$$ $$\varphi'(a)=1-\frac{g(a)}{m\cdot g(a)+0}-0=1-\frac{1}{m}\neq0$$

为了提高收敛的阶，可取 $\varphi(x)=x-m\frac{f(x)}{f’(x)}$，从而 $\varphi(a)=1-\frac{m}{m}=0$，则新迭代法至少是平方收敛的

例题

*多根区间上的逐次逼近法(应该不会考)

这里主要使用二分法

4.3 幂法

参考 幂法与反幂法 - 知乎 (zhihu.com)

幂法（用于求绝对值最大的特征值）

幂法用于计算绝对值最大的特征值和对应的特征向量，对于单根和重根情形均有效。

概念：假定 n 阶方阵 A 具有 n 个线性无关的特征向量 $x_1,x_2,\cdots,x_n$，且对应的特征值满足 $|\lambda_1|>|\lambda_2|\geq\cdots\geq|\lambda_n|$，则对任一 n 维非零向量 $v_0$ 经使用迭代过程

$$v_k=A^kv_0$$

计算可得

$$v_k=\alpha_1\lambda_1^kx_1,\quad \alpha_1\neq0,\quad \frac{v_k}{v_{k-1}}=\lambda_1$$

实际使用上，对幂法进行了改进，添加了规范化操作

算法过程

1. 输入矩阵 $A=(a_{ij})$，初始向量 $v_0$，允许的误差 $\epsilon$，最大迭代次数 $N$
2. 置 $k=1,\quad \mu=0$
3. 求 $\max\{v_k\},\quad\max\{v_k\}\Rightarrow a$
4. 计算 $u=v/a,\quad v=Au$，置 $\max\{v_k\}=\lambda$
5. 若 $|\lambda-\mu|<\epsilon$，输出 $\lambda,u$，停机，否则跳转至 6
6. 若 $k<N$，置 $k+1\Rightarrow k,\lambda\Rightarrow\mu$，转到 3，否则输出失败信息，停机

例题

利用幂法计算矩阵 A 的主（最大）特征值和相应的特征向量，其中 $A=\begin{pmatrix}2&3&2\\10&3&4\\3&6&1\end{pmatrix}$，取 $v_0=(0,0,1)^T$，迭代2次

解：

取 $u_0=v_0=(0,0,1)^T$，则 $u_1=Av_0=(2,4,1)^T$，且 $\max\{u_1\}=-4$

即 $a=4$，于是 $v_1=u_1/a=(0.5,1,0.25)^T$

$u_2=Av_1=(4.5,9,7.75)^T$ 且 $\max\{u_2\}=9$

即 $a=9$，于是 $v_2=u_2/a\approx(0.5,1,0.8611)$，可得 $\lambda_1\approx9,x_1\approx(0.5,1.0,0.8611)^T$

注：经过 8 次迭代可得 $\lambda_1=11,x_1=(0.5,1.0,0.75)^T$

反幂法

反幂法用于计算矩阵 A 按模最小的特征值及对应的特征向量

算法流程：

1. 任取初始向量 $v_0=u_0\neq0$
2. 计算 $v_k=A^{-1}u_{k-1},\;(k=1,2,\cdots)$
3. $\max\{v_k\}\Rightarrow m_k;\quad u_k=v_k/m_k$
4. 如果 $k$ 从某时以后有 $\frac{(v_k)_j}{(v_{k-1})_j}\approx c \;\;(常数)(j=1,2,\cdots,n)$，则取 $\lambda_n\approx\frac{1}{c}$；而 $u_k$ 就是与 $\lambda_k$ 对应的特征向量

例题

1

用反幂法求矩阵 $A=\begin{pmatrix}3&2\\4&5\end{pmatrix}$ 的按模最小的特征值和特征向量，精确至 6 位小数，迭代 1 次

解：

取 $v_0=u_0=(1,1)^T$，由 $v_1=A^{-1}u_0$，即 $Av_1=u_0$

得 $v_1=(0.428571,-0.142857)^T\\m_1=\max\{v_1\}=0.428571$

归一化得 $u_1=(1.000000,-0.333333)^T$

所以迭代 1 次得到的按模最小的特征值为 $1/0.428571$，对应的特征向量为 $u_1=(1.000000,-0.333333)^T$

2

用反幂法求矩阵 $A=\begin{pmatrix}3&2\\4&5\end{pmatrix}$ 的过程中，得到 $u^{(8)}=\begin{pmatrix}1.000000\-0.999999\end{pmatrix}$，则 A 的模最小的特征值的近似值为：

解：

由于 $c=\max(u^{(8)}=1)$，则按模最小的特征值的近似值为 $\lambda_1=\frac{1}{c}=1.000000$

或者

依据特征值的概念与性质，可知有 $Ax=\lambda x$，则

$$Au^{(8)}=\lambda_nu^{(8)}\approx \begin{pmatrix} 1\\-1 \end{pmatrix}$$

则，可认为按模最小的特征值的近似值为 1。

4.4 共轭梯度法

共轭梯度法是以共轭方向作为搜索方向的一类算法，最初用于求解线性方程组，后来用于求解无约束最优化问题，是一种重要的数学优化方法。

*最速下降法（应该不会考）

共轭梯度法

下降方向 p 为上步下降方向与当前残量的线性组合，与 $\beta$ 有关，步长为 $\alpha$

共轭梯度法最多迭代 n 步即可求得问题的精确解

算法的流程：

对于所给的初始向量 $x_0$，$r_0=p_0=b-Ax_0$

$$\alpha_k=(r_k,r_k)/(Ap_k,p_k)\\ x_{k+1}=x_k+\alpha_kp_k\\ r_{k+1}=r_k-\alpha_kAp_k\\ \beta_k=(r_{k+1},r_{k+1})/(r_k,r_k)\\ p_{k+1}=r_{k+1}+\beta_kp_k\\ (k=0,1,2,\cdots)$$

$(r_k,r_k)$ 表示内积运算。

例题

可见，迭代 2 步即可得到精确解

END