2022-2023 春学期 矩阵与数值分析 C3 矩阵分析基础

引言

本文内容来自于对矩阵与数值分析课程资料的整理；

本文所涉及的课程指东北某沿海高校，计算机学院硕士生必修课“矩阵与数值分析”，课程资料包括课程PPT、教材《计算机科学计算 第二版》¹，以及网络资料，师兄的笔记等。

¹. 《计算机科学计算 第二版》 作者: 张宏伟 金光日 施吉林；出版社: 高等教育出版社；页数: 379；定价: 38.1元；装帧: 平装-胶订；ISBN: 9787040365955 出版年：2013；学科主题: 电子计算机 教材 科学计算-高等学校；中图法分类号: TP301.6； 一般附注: 高等学校教材 ↩

C3 矩阵分析基础

3.1 矩阵序列与级数

矩阵序列相关定义与特性

矩阵序列：按整数 k 的序列，将 $C^{m\times n}$ 中的矩阵排成一列 $A_1,A_2,A_3,\cdots,A_k,\cdots$，称这列有序的矩阵为矩阵为矩阵序列，称 $A_k$ 为矩阵序列的一般项。

矩阵序列的发散与收敛：$\{A_k\}^\infty_{k=1}$ 为 $C^{m\times n}$ 中的矩阵序列，其中 $A_k=(a_{ij}^{(k)})$，又 $A=a_{ij}\in C^{m\times n}$，如果 $\lim\limits_{k\rightarrow\infty}a^{(k)}_{ij}=a_{ij}$，对 $i=1,2,\cdots,m;j=1,2,\cdots,n$ 均成立，则称矩阵序列 $\{A_k\}^\infty_{k=1}$ 收敛，而 A 称为矩阵序列 $\{A_k\}^\infty_{k=1}$ 的极限，记为 $\lim\limits_{k\rightarrow\infty}A_k=A$；不收敛的矩阵序列称为发散的。

可见矩阵序列收敛和矩阵中的元素都收敛的是相互充要的。

矩阵序列收敛性与范数：设 $\{A_k\}^\infty_{k=1}$ 为 $C^{m\times n}$ 中的矩阵序列，$||\cdot||$ 为 $C ^{m\times n}$ 中的一种矩阵范数，则矩阵序列 $\{A_k\}^\infty_{k=1}$ 收敛于 A 的充要条件是 $||A_k-A||$ 收敛于零。

相关结论：设 $\{A_k\}^\infty_{k=1},A\in C ^{m\times n}$ ，并且 $\lim\limits_{k\rightarrow\infty}A_k=A$，则 $\lim\limits_{k\rightarrow\infty}||A_k||=||A||$；此结论只是充分条件，反过来不一定成立。

对于矩阵序列的四则运算，有：

设 $\{A_k\}^\infty_{k=1}$, 和 $\{B_k\}^\infty_{k=1}$，分别为$ C ^{m\times n}$ 和 $ C ^{n\times l}$，并且 $\lim\limits_{k\rightarrow\infty}A_k=A,\lim\limits_{k\rightarrow\infty}B_k=B$，则

• $\lim\limits_{k\rightarrow\infty}(\alpha A_k+\beta B_k)=\alpha A+\beta B,\forall\alpha,\beta\in C$
• $\lim\limits_{k\rightarrow\infty}A_kB_k=AB$
• 设 $\{A_k\}^\infty_{k=1},A\in C ^{n\times n}$ 中的矩阵序列，并且 $\lim\limits_{k\rightarrow\infty}A_k=A,A_k(k=1,2,\cdots)$，和 $A\in C ^{n\times n}$ 均为可逆矩阵，则 $\lim\limits_{k\rightarrow\infty}A^{-1}=A^{-1}$；注意矩阵序列可逆不能保证极限一定可逆
• 可逆矩阵极限可能奇异，非零矩阵极限可能为零

收敛矩阵：$A\in C^{n\times n},\lim\limits_{k\rightarrow\infty}A^k=0$

定理：$\rho(A)<1$ 的充要条件是：存在 $C^{n\times n}$ 上的某种范数 $||\cdot||$ ，使得 $||A||<1$

定理：设 $C^{n\times n}$，$\lim\limits_{k\rightarrow\infty}A^k=0$ 的充分必要条件是存在 $C^{n\times n}$ 上的某种范数 $||\cdot||$ ，使得 $||A||<1$

所以有：

$\rho(A)<1\Leftrightarrow\lim\limits_{k\rightarrow\infty}A^k=0\Leftrightarrow任意 ||A||<1$

判断一个矩阵是否为收敛矩阵：

• 若 $A^k$ 容易计算，则利用其判断收敛性
• 判断矩阵的某种范数是否小于 1
• 计算矩阵的谱半径

例题

矩阵级数相关定义与结论

定义：设 $\{A_k\}^\infty_{k=1}$ 为 $C ^{m\times n}$ 中的矩阵序列，称

$$A_1+A_2+\cdots+A_k+\cdots$$

为由矩阵序列 $\{A_k\}^\infty_{k=1}$ 构成的矩阵级数，记为 $\sum\limits^\infty_{k=1}A_k$

定义：记 $S_k=\sum\limits^k_{i=1}A_i$，称之为矩阵级数 $\sum\limits^\infty_{k=1}A_k$ 的前 k 项部分和，若矩阵序列 $\{S_k\}^\infty_{k=1}$ 收敛且 $\lim\limits_{k\rightarrow\infty}S_k=S$，则称矩阵级数 $\sum\limits^\infty_{k=1}A_k$ 收敛；矩阵 S 称为矩阵级数的和函数，记为 $S=\sum\limits^\infty_{k=1}A_k$。不收敛的矩阵级数称为发散的。矩阵级数收敛即 $m\times n$ 个数项级数 $\sum\limits^\infty_{k=1}a_{ij}^{(k)}$ 均收敛。

定理：设 A 为 n 阶方阵，则 $\sum\limits_{k=0}^\infty A^k=I+A+A^2+\cdots+A^k+\cdots$ 收敛（$A^0=I$）的充要条件是 $\rho(A)<1$

定理：设 A 为 n 阶方阵，当 $\sum\limits_{k=0}^\infty A^k$ 收敛时，有 $\sum\limits_{k=0}^\infty A^k=(I-A)^{-1}$，而且存在 $C^{n\times n}$ 上的算子范数 $||\cdot||$，使得 $||(I-A)^{-1}-\sum\limits^m_{k=0}A^k||\leq\frac{||A||^{m+1}}{1-||A||}$

例题

矩阵级数绝对收敛相关结论

定义：设 $\sum\limits_{k=1}^\infty A_k$ 为 $C^{m\times n}$ 中的矩阵级数，其中 $A_k=(a^{(k)}_{ij})$。如果$\sum\limits_{k=1}^\infty a_{ij}^{(k)}$ 对任意的 $1\leq i\leq m,\, 1\leq j\leq n$ 均为绝对收敛的，则称矩阵级数 $\sum\limits_{k=1}^\infty A_k$ 绝对收敛。

定理：矩阵级数 $\sum\limits_{k=1}^\infty A_k$ 为绝对收敛的充要条件是正项级数 $\sum\limits_{k=1}^\infty ||A_k||$收敛

定理：若矩阵级数 $\sum\limits_{k=1}^\infty A_k$ 是绝对收敛的，则它一定是收敛的，并且任意调换各项的顺序所得到的级数还是收敛的，且级数和不变；显然，收敛的级数不一定绝对收敛，而绝对收敛的级数一定是收敛的。

定理：设 $\sum\limits_{k=1}^\infty A_k$ 为 $C^{m\times n}$ 中的绝对收敛的矩阵级数，$A=\sum\limits_{k=1}^\infty A_k$，设 $\sum\limits_{k=1}^\infty B_k$ 为 $C^{n\times l}$ 中的绝对收敛的矩阵级数，$B=\sum\limits_{k=1}^\infty B_k$，则 $\sum\limits_{k=1}^\infty A_k\cdot\sum\limits_{k=1}^\infty B_k$ 按任何方式排列得到的级数绝对收敛，且和为 AB。

定理，设 $P\in C^{p\times m}$ 和 $Q\in C^{n\times q}$ 为给定矩阵，则 $\sum\limits_{k=0}^\infty A_k$ 收敛可以得到 $\sum\limits_{k=0}^\infty PA_kQ$ 收敛； $\sum\limits_{k=0}^\infty A_k$ 绝对收敛可以得到 $\sum\limits_{k=0}^\infty PA_kQ$ 绝对收敛；且有等式 $P(\sum\limits_{k=0}^\infty A_k)Q$

3.2 幂级数

收敛与发散

矩阵幂级数的一般形式：$\sum\limits_{k=0}^\infty a_kA^k$

定理：设 $\sum\limits^\infty_{k=0}a_kt^k$ 为收敛半径为 r 的幂级数，A 为 n 阶方阵，则

• $\rho(A)<r$ 时，矩阵幂级数 $\sum\limits_{k=0}^\infty a_kA^k$ 绝对收敛
• $\rho(A)>r$ 时，矩阵幂级数 $\sum\limits_{k=0}^\infty a_kA^k$ 发散

定理：设 $\sum\limits_{k=0}^\infty a_k(z-z_0)^k$ 为收敛半径为 r 的幂级数，A 为 n 阶方阵，

• 如果 A 的特征值均落在收敛圆内，即 $|\lambda-z_0|<r$，其中 $\lambda$ 为任意特征值，则矩阵幂级数 $\sum\limits_{k=0}^\infty a_k(A-z_0I)^k$ 绝对收敛
• 若有某个 $\lambda_{i_0}$ 使得 $|\lambda_{i_0}-z_0|>r$，则幂级数 $\sum\limits_{k=0}^\infty a_k(A-z_0I)^k$ 发散

幂级数与解析函数的关系

利用 Jordan 分解计算矩阵函数

定理：设 $f(z)=\sum\limits^\infty_{k=0}a_kz^k$ 是收敛半径为 r 的幂级数，J 是特征值为 $\lambda$ 的 n 阶 Jordan 块阵，且 $|\lambda|<r$，则

$$f(J)= \begin{pmatrix} f(\lambda)&f'(\lambda)&\cdots&\frac{f^{(n-1)}(\lambda)}{(n-1)!}\\ &f(\lambda)&\ddots&\vdots\\ &&\ddots&f'(\lambda)\\ &&&f(\lambda) \end{pmatrix}$$

定理：设 $f(z)=\sum\limits^\infty_{k=0}a_k(z-z_0)^k$ 是收敛半径为 r 的幂级数，J 是特征值为 $\lambda$ 的 n 阶 Jordan 块阵，且 $|\lambda-z_0|<r$，则

$$f(J)= \begin{pmatrix} f(\lambda)&f'(\lambda)&\cdots&\frac{f^{(n-1)}(\lambda)}{(n-1)!}\\ &f(\lambda)&\ddots&\vdots\\ &&\ddots&f'(\lambda)\\ &&&f(\lambda) \end{pmatrix}$$

定理：设 $f(z)=\sum\limits^\infty_{k=0}a_kz^k$ 是收敛半径为 r 的幂级数，J 是特征值为 $\lambda$ 的 n 阶 Jordan 块阵，且 $|t\lambda|<r$，则

$$f(tJ)= \begin{pmatrix} f(t\lambda)&tf'(\lambda)&\cdots&\frac{t^{(n-1)}f^{(n-1)}(t\lambda)}{(n-1)!}\\ &f(t\lambda)&\ddots&\vdots\\ &&\ddots&tf'(\lambda)\\ &&&f(t\lambda) \end{pmatrix}$$

定理（利用矩阵的 Jordan 分解求矩阵函数 f(A) 的具体表达式）：设 $f(z)=\sum\limits^\infty_{k=0}a_k(z-z_0)^k$ 为收敛半径为 r 的幂级数，A 为 n 阶方阵，$A=TJT^{-1}$ 为其 Jordan 分解， $J=\mathrm{diag}(J_1,J_2,\cdots,J_s)$；当 A 的特征值均落在收敛圆内时，即 $|\lambda-z_0|<r$，其中 $\lambda$ 为 A 的任意特征值，则矩阵幂级数 $\sum\limits^\infty_{k=0}a_k(z-z_0)^k$ 绝对收敛，并且和矩阵为:

$$f(A)=T\mathrm{diag}(f(J_1),f(J_2),\cdots,f(J_s))T^{-1}$$

其中 $f(J_i)$ 的定义如前表达式。

注意，若 A 的特征值为 $\lambda_1,\lambda_2,\cdots,\lambda_n$，则 f(A) 的特征值应为 $f(\lambda_1),f(\lambda_2),\cdots,f(\lambda_n)$

计算矩阵函数值的基本步骤：

1. 计算 Jordan 分解 $A=TJT^{-1}=T\mathrm{diag}(J_1,\cdots,J_s)T^{-1}$
2. 求 $f(A)=T\mathrm{diag}(f(J_1),\cdots,f(J_s))T^{-1}$

例题

已知 $J_i=\begin{pmatrix}-1&1&&\ &-1&1\\&&-1&1\\&&&-1\end{pmatrix}$，求 $e^{J_i},\;e^{tJ_i}$

解：

$$e^{J_i}= \begin{pmatrix} e^{-1}&e^{-1}&\frac{e^{-1}}{2}&\frac{e^{-1}}{6}\\ &e^{-1}&e^{-1}&\frac{e^{-1}}{2}\\ &&e^{-1}&e^{-1}\\ &&&e^{-1} \end{pmatrix}\\ e^{tJ_i}= \begin{pmatrix} e^{-t}&te^{-t}&\frac{t^2e^{-t}}{2}&\frac{t^3e^{-t}}{6}\\ &e^{-t}&te^{-t}&\frac{t^2e^{-t}}{2}\\ &&e^{-t}&te^{-t}\\ &&&e^{-t} \end{pmatrix}$$

求 sinA，sinAt，其中

$$A= \begin{pmatrix} 1&&&\\ &2&&\\ &&3&\\ &&&4\\ \end{pmatrix},\; \sin A= \begin{pmatrix} \sin1&&&\\ &\sin2&&\\ &&\sin3&\\ &&&\sin4\\ \end{pmatrix},\; \sin At= \begin{pmatrix} \sin t&&&\\ &\sin2t&&\\ &&\sin3t&\\ &&&\sin4t\\ \end{pmatrix};\\ A= \begin{pmatrix} 1&&&\\ &1&&\\ &&1&\\ &&&1\\ \end{pmatrix},\; \sin A= \begin{pmatrix} \sin1&&&\\ &\sin1&&\\ &&\sin1&\\ &&&\sin1\\ \end{pmatrix},\; \sin At= \begin{pmatrix} \sin t&&&\\ &\sin t&&\\ &&\sin t&\\ &&&\sin t\\ \end{pmatrix};\\ A= \begin{pmatrix} 1&&&\\ &1&1&\\ &&1&1\\ &&&1\\ \end{pmatrix},\; \sin A= \begin{pmatrix} \sin1&&&\\ &\sin1&\cos1&-\frac{\sin1}{2}\\ &&\sin1&\cos1\\ &&&\sin1\\ \end{pmatrix},\; \sin At= \begin{pmatrix} \sin t&&&\\ &\sin t&t\cos t&-\frac{t^2\sin t}{2}\\ &&\sin t&t\cos t\\ &&&\sin t\\ \end{pmatrix};\\$$

有限待定系数法

问题：给定函数 f(x)，计算 f(Ax)

挑战：为避免计算矩阵的 Jordan 分解

$$f(\lambda t)=p(\lambda,t)\psi(\lambda)+q(\lambda,t)$$

$\psi(\lambda)$ 为特征多项式，$q(\lambda,t)$ 为次数不超过 n-1 的含参多项式

$$\psi(\lambda)=\det(A-\lambda I),\\ q(\lambda,t)=b_{n-1}(t)\lambda^{n-1}+\cdots+b_1(t)\lambda+b_0(t)$$

有 Hamilton-Catley 定理可知 $\psi(A)=0$，从而

$$f(At)=q(A,t)$$

关键：确定含参系数 $b_{n-1}(t),\cdots,b_1(t),b_0(t)$

显然，A 的特征多项式

$$\psi(\lambda)=\det(A-\lambda I)=\prod\limits^s_{i=1}(\lambda-\lambda_i)^{m_i}\Rightarrow\psi^{(j)}(\lambda_i)=0,\; j=0,\cdots,m_j-1,\; i=1,\cdots,s$$

故将 $f(\lambda t)=p(\lambda,t)\psi(\lambda)+q(\lambda,t)$ 两端对 $\lambda$ 求导，得到

$$\begin{aligned} f(\lambda t)&=p(\lambda,t)\psi(\lambda)+q(\lambda,t)\\ &\Rightarrow \left . \frac{\mathrm{d}^j}{\mathrm{d}\lambda^j}f(\lambda t)\right|_{\lambda=\lambda_i}=\left . \frac{\mathrm{d}^j}{\mathrm{d}\lambda^j}q(\lambda,t)\right|_{\lambda=\lambda_i}\\ &\Rightarrow \left . t^j\frac{\mathrm{d}^j}{\mathrm{d}u^j}f(u)\right|_{u=\lambda_it}=\left . \frac{\mathrm{d}^j}{\mathrm{d}\lambda^j}q(\lambda,t)\right|_{\lambda=\lambda_i} \end{aligned}$$

n 个方程，n 个变量的线性方程组

待定系数法的步骤：

1. 计算 A 的特征多项式 $\psi(\lambda)=\det(A-\lambda I)$

2. 定义 $q(\lambda,t)=b_{n-1}(t)\lambda^{n-1}+\cdots+b_1(t)\lambda+b_0(t)$

   利用(可假设 t=1)

   $$\left . \frac{\mathrm{d}^j}{\mathrm{d}\lambda^j}f(\lambda t)\right|_{\lambda=\lambda_i}=\left . \frac{\mathrm{d}^j}{\mathrm{d}\lambda^j}q(\lambda,t)\right|_{\lambda=\lambda_i} \quad或\quad \left . t^j\frac{\mathrm{d}^j}{\mathrm{d}u^j}f(u)\right|_{u=\lambda_it}=\left . \frac{\mathrm{d}^j}{\mathrm{d}\lambda^j}q(\lambda,t)\right|_{\lambda=\lambda_i}$$

   确定含参系数 $b_{n-1}(t),\cdots,b_1(t),b_0(t)$

3. 计算(假设 t=1，f(A)=q(A)) $f(At)=q(A,t)$

例题

矩阵函数等式

若 $\forall A \in C^{n\times n}$，总有：

• $\sin(-A)=-\sin A,\cos(-A)=\cos A$
• $e^{iA}=\cos A+i\sin A,\, \cos A=\frac{1}{2}(e^{iA}+e^{-iA}),\,\sin A=\frac{1}{2i}(e^{iA}-e^{-iA})$

若 $A,B\in C^{n\times n}$，且 AB=BA，则

• $e^Ae^B=e^Be^A=e^{A+B}$
• $\sin(A+B)=\sin A\cos B+\cos A\sin B$
• $\cos(A+B)=\cos A\cos B-\sin A\sin B$

若 A=B，则 $cos2A=\cos^2A-\sin^2A,\,\sin2A=2\sin A\cos A$

对任何 n 阶方阵 A，$e^A$ 总是可逆矩阵

$$e^Ae^{-A}=e^{-A}e^A=e^0=I$$

sinA 和 cosA 不一定可逆，例如：

$$A=\begin{pmatrix} \pi&0\\0&\frac{\pi}{2} \end{pmatrix} \\ \sin A=\begin{pmatrix}\sin\pi&0\\0&\sin\frac{\pi}{2}\end{pmatrix}=\begin{pmatrix}0&0\\0&1\end{pmatrix} \\\cos A=\begin{pmatrix}\cos\pi&0\\0&\cos\frac{\pi}{2}\end{pmatrix}=\begin{pmatrix}-1&0\\0&0\end{pmatrix}$$

其他若干结论：

• $f(A^T)=f(A)^T$
• $\det(e^A)=e^{trA}$
• $(e^{A})^{-1}=e^{-A}$
• $||e^A||\leq e^{||A||}$
• 若 A 为 Hermite 阵，则 $e^{iA}$ 是酉阵

例题

3.3 矩阵的微积分

含参矩阵微分

元素为函数的矩阵微分：如果矩阵 $A(t)=(a_{ij}(t))_{m\times n}$ 的每一个元素 $a_{ij}(t),i=1,2,\cdots,m;j=1,2,\cdots,n$，在[a,b] 上均为变量 t 的可微函数，则称 A(t) 可微，且导数定义为(也就是针对每个矩阵元素对 t 求导):

$$A'(t)=\frac{d}{dt}A(t)=(\frac{d}{dt}a_{ij}(t))_{m\times n}$$

求导法则：

设 A(t), B(t) 是可进行运算的两个可微矩阵，则

• $(A(t)+B(t))’=A’(t)+B’(t)$
• $(A(t)B(t))’=A’(t)B(t)+A(t)B’(t)$
• $(\alpha A(t))’=\alpha\cdot A’(t)$，其中 $\alpha$ 为任意常数
• 当 $A^{-1}(t)$ 为可微矩阵时，有 $(A^{-1}(t))’=-A^{-1}(t)A’(t)A^{-1}(t)$
• 当 $u=f(t)$ 关于 t 可微时，有 $(A(u))’=f’(t)\frac{d}{du}A(u)$

函数矩阵的高阶导数定义为：

$$\frac{d^k}{dt^k}(A(t))=\frac{d}{dt}(\frac{d^{k-1}}{dt^{k-1}}(A(t)))$$

注：$(A^m(t))’=mA^{m-1}(t)(A(t))’$ 不一定成立, $A(t)(A(t))’\neq(A(t))’A(t)$, 事实上 $(A^2(t))’=(A(t)A(t))’=A’(t)A(t)+A(t)A’(t)\neq2A’(t)A(t)$

特殊矩阵函数导数

设 n 阶方阵 A 与 t 无关，则有：

• $(e^{tA})’=Ae^{tA}=e^{tA}A$
• $(\sin(tA))’=A\cdot\cos(tA)=\cos(tA)\cdot A$
• $(\cos(tA))’=-A\cdot\sin(tA)=-\sin(tA)\cdot A$

重要的例题

可利用特殊点的导数值求相应矩阵

例题

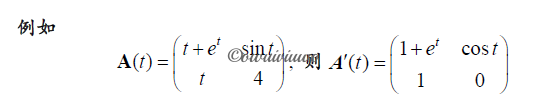
矩阵函数积分

如果矩阵 $A(t)=(a_ij(t))_{m\times n}$ 的每一个元素 $a_ij(t)$ 都是区间 $[t_0,t_1]$ 上的可积函数，则定义 A(t) 在区间 $[t_0,t_1]$ 上的积分为（对矩阵积分也就是对矩阵中每个元素积分）：

$$\int^{t_1}_{t_0}A(t)dt=(\int^{t_1}_{t_0}a_{ij}(t)dt)_{m\times n}$$

性质（与函数的积分类似）

• $\int^{t_1}_{t_0}(\alpha A(t)+\beta B(t))dt=\alpha\int^{t_1}_{t_0}A(t)dt+\beta\int^{t_1}_{t_0} B(t))dt,\;\forall\alpha,\beta\in C$

• $\int^{t_1}_{t_0}(A(t)B)dt=\int^{t_1}_{t_0}A(t)dtB$ 其中 B 为常数矩阵

  $\int^{t_1}_{t_0}(AB(t))dt=A\int^{t_1}_{t_0}B(t)dt$ 其中 A 为常数矩阵

• 当 A(t) 在 [a,b] 上连续可微时，对任意 $t\in(a,b)$ ，有 $\frac{d}{dt}(\int^{t}_{a}A(\tau)d\tau)=A(t)$

• 当 A(t) 在 [a,b] 上连续可微时，对任意 $t\in(a,b)$ ，有 $\int^{b}_{a}\frac{dA(t)}{dt}dt=A(b)-A(a)$

* 相对于矩阵变量的微分

应该不会考 :)

函数对矩阵求导：设 $X=(x_{ij})_{m\times n}$，函数 $f(X)=f(x_{11},x_{12},\cdots,x_{1n},x_{21},\cdots,x_{mn})$ 为 mn 元的多元函数，且 $\frac{\partial{f}}{\partial{x_{ij}}}(i=1,2,\cdots,m;j=1,2,\dots,n)$ 都存在，定义 f(X) 对矩阵 X 的导数为：

$$\frac{d}{dX}f(X)=(\frac{\partial{f}}{\partial{x_{ij}}})_{m\times n}= \begin{pmatrix} \frac{\partial{f}}{\partial{x_{ij}}}&\cdots&\frac{\partial{f}}{\partial{x_{ij}}}\\ \cdots&\ddots&\cdots\\ \frac{\partial{f}}{\partial{x_{ij}}}&\cdots&\frac{\partial{f}}{\partial{x_{ij}}} \end{pmatrix}$$

例题

* 微分方程组相关内容

应该不会考 :)

可参考第七章的内容

一阶线性常系数齐次微分方程组

问题描述

解的存在性

解的唯一性

一阶线性常系数非齐次微分方程组

问题描述

解的存在性

例题

END