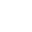2022-2023 春学期 矩阵与数值分析 C1 绪论
引言
本文内容来自于对矩阵与数值分析课程资料的整理;
本文所涉及的课程指东北某沿海高校,计算机学院硕士生必修课“矩阵与数值分析”,课程资料包括课程PPT、教材《计算机科学计算 第二版》1,以及网络资料,师兄的笔记等。
1. 《计算机科学计算 第二版》 作者: 张宏伟 金光日 施吉林;出版社: 高等教育出版社;页数: 379;定价: 38.1元;装帧: 平装-胶订;ISBN: 9787040365955 出版年:2013;学科主题: 电子计算机 教材 科学计算-高等学校;中图法分类号: TP301.6; 一般附注: 高等学校教材 ↩
C1 绪论
1.1 计算机科学计算研究对象与特点
该部分介绍了计算机科学计算研究对象与特点;

1.2 误差分析与数值方法的稳定性
误差的来源与分类


误差基本概念与有效数字
相对与绝对误差:
- 绝对误差:设 x 为精确值,a 为 x 的一个近似值,称 x-a 为近似值 a 的绝对误差,简称误差。误差 x-a 可正可负。通常准确值 x 是未知的,因此 x-a 也是未知的。
- 绝对误差界:设 x 为精确值,a 为 x 的一个近似值,若有常数 $e_a$ 使得 $|x-a|\leq e_a$ ,则 $e_a$ 叫做近似值 a 的误差界(限)。它总是正数。显然有 $a-e_a\leq x\leq a+e_a$。
- 相对误差:若 $x\neq0$,则将近似值的误差与准确值的比值$\frac{x-a}{x}$ 称为近似值 a 的相对误差。相对误差也可正可负。实际计算中,如果真值 x 未知时,通常取 $ \frac{x-a}{x} \approx \frac{x-a}{a}$ 作为 a 的相对误差,条件是 $\frac{x-a}{x}$ 较小。
- 相对误差界(限):相对误差的绝对值上限叫做相对误差界(限),记为 $\frac{x-a}{a}\leq\frac{e_a}{|a|}$。
误差界的取法:当准确值 x 的位置比较多时,人们常常按照四舍五入的原则得到 x 的前几位近似值 a。
* 例如:
$x = \pi = 3.1415926\cdots$
取3位:$a_1 = 3.14, \pi-a_1=0.00159265\cdots$
取5位:$a_2 = 3.1416,\pi-a_2=-0.00000735\cdots$
那么它们的误差界的取法应为:
$|\pi-3.14|\leq\frac{1}{2}\times 10^{-2}, |\pi-3.1416|\leq\frac{1}{2}\times10^{-4}$
有效数字相关
定义:设 x 为精确值,a 为 x 的一个近似值 ,a 由 n 位数组成,自左向右第 i 位为$a_i$,是 0 到 9 之中的一个数字,且$i\geq1, a_1\neq 0$,表示为: $a = \pm 10^k\times0.a_1a_2\cdots a_n\cdots$,其中,n 为正整数,k 为整数,如果其绝对误差界 $|x-a|\leq\frac{1}{2}\times 10^{k-n}$,则称 a 为 x 的具有 n 位有效数字的近似值
有关结论:
- 有效数字位数与小数点的位置无关
- 一般来说,绝对误差与小数位数有关,相对误差与有效数字位数有关
- 如果一个近似值是由精确值四舍五入得到的,那么,从这个近似值的末尾数向前数起直至在五非零数字位置,所属到的数字均为有效数字
求有效数字位数的步骤:首先将近似值表示为定义中 a 的形式,可以得到 k,接下来一句上述定义计算绝对误差界,得到 k-n ,最后即可依据上述数据得到有效数字位数 n 。
* 例如1:
对于 $ e = 2.71828182\cdots$,下面各个值的有效数字的位数。
取 $a=2.718 = 10^1\times 0.2718, k=1$,
其绝对误差界为 $|e-a|<0.0003<\frac{1}{2}\times10^{-3}, k-n=-3, n=4$,
$a$ 是 $e$ 的具有4位有效数字的近似值。
取 $a_1=2.7182 = 10^1\times 0.27182, k=1$,
其绝对误差界为 $|e-a_1|<0.00009<\frac{1}{2}\times10^{-3}, k-n=-3, n=4$,
$a_1$ 是 $e$ 的具有4位有效数字的近似值。
* 例如2:
下列近似值的绝对误差界均为 0.005,问其有效数字的位数。
$a=138.00, b=-0.0312, c=0.86\times 10 ^{-4}$
对于$a$, $|x-a|<\frac{1}{2}\times10^{-2}, k-n=-2$,且 $a=138.00=0.138\times10^3, k=3, n=5$,a 具有5位有效数字。
对于$b$, $|x-b|<\frac{1}{2}\times10^{-2}, k-n=-2$,且 $b=-0.0312=-0.312\times10^{-1}, k=-1, n=1$,b 具有1位有效数字。
对于$c$, $|x-c|<\frac{1}{2}\times10^{-2}, k-n=-2$,且 $c=0.86\times 10^{-4}, k=-4, n=-2$,不满足 $n$ 为正整数的条件,故 c 具有0位有效数字。
有效数字与相对误差界
关于有效数字与相对误差界有如下定理:
若实数 x 为某个精确值, a 为它的一个近似值,其表达式形式如
$a=\pm10^k\times0.a_1a_2\cdots a_n\cdots$
- 如果 a 有 n 位有效数字,则其相对误差满足 $\frac{|x-a|}{|a|}\leq\frac{1}{2a_1}\times10^{1-n}$.
- 如果其相对误差满足 $\frac{|x-a|}{|a|}\leq\frac{1}{2(a_1+1)}\times10^{1-n}$,则 a 至少有 n 位有效数字。
其推导过程如下所示:

函数计算的误差估计
针对一元函数:
思路:使用 Taylor 展开计算解决这一问题,例如将 f(x) 在 x=a 展开:
$ f(x)=f(a)+f(a)’(x-a) + \frac{f’’(\xi)(x-a)}{2}$
$ |f(x)-f(a)|\leq|f’(a)||x-a|+\frac{|f’’(xi)||(x-a)|^2}{2}$
由上式可得,
近似绝对误差估计式为:$|f(x)-f(a)|\approx|f’(a)||x-a|$
近似相对误差界为:$\frac{|f(x)-f(a)|}{|f(a)}\leq\frac{f’(a)}{f(a)}|x-a|$
* 例如1
计算 $\sqrt{a}$ 的相对误差界
解: 相对误差界为
$\frac{\sqrt{x}-\sqrt{a}}{\sqrt{a}}\leq\frac{(\sqrt{x})’|_{x=a}}{\sqrt{a}}|x-a|=\frac{1}{2(\sqrt{a})^2}|x-a|=\frac{1}{2}\frac{|x-a|}{|a|}$
可知,$\sqrt{a}$ 的相对误差为 $a$ 的相对误差的一半
类似的,针对多变元的情况,
如果 $f(x_1,x_2,\cdots,x_n)$ 为 $n$ 元函数,自变量 $x_1,x_2,\cdots,x_n$ 的近似值为 $a_1,a_2,\cdots,a_n$ ,
则 $f(x_1,x_2,\cdots,x_n)-f(a_1,a_2,\cdots,a_n)\approx\sum^n_{k=1}(\frac{\partial f}{\partial x_k})_a(x_k-a_k)$
的函数值的误差界 $|f(x_1,x_2,\cdots,x_n)-f(a_1,a_2,\cdots,a_n)|\approx\sum^n_{k=1}|(\frac{\partial f}{\partial x_k})_a||x_k-a_k|$
* 例如2
可利用上述定义计算四则运算的误差估计
$|f(x_1,x_2)-f(a_1,a_2)|\leq|(\frac{\partial f}{\partial x_1})_{a}|\cdot |x_a-a_1|+|(\frac{\partial f}{\partial x_2})_{a}|\cdot |x_2-a_2|$
针对加减法 $f(x_1,x_2)=x_1\pm x_2$, 有 $ |(x_1\pm x_2)-(a_1\pm a_2)|\leq|x_1-a_1|+|x_2-a_2|$
可知:两个近似数相加减,其运算结果的精度不必原始数据的任何一个精度高。
注意:在计算中应避免两个相近的数相减,否则容易导致有效数字的损失
针对乘法 $f(x_1,x_2)=x_1\cdot x_2$,有 $|x_1x_2-a_1a_2|\leq |a_2||x_1-a_1|+|a_1||x_2-a_2|$
针对除法 $f(x_1,x_2)=\frac{x_1}{x_2}$,有 $|\frac{x_1}{x_2}-\frac{a_1}{a_2}|\leq\frac{|x_1-a_1|}{|a_2|}+\frac{|a_1||x_2-a_2|}{|a_2|^2}\leq\frac{|a_2||x_1-a_1|+|a_1||x_2-a_2|}{|a_2|^2}$
可知,计算中应尽力避免小数作除数
数值方法数值稳定性
定义:
用某一种数值方法求一个问题的数值解,如果在方法的计算过程中舍入误差在一定条件下能够得到控制(或者说舍入误差增长不影响产生可靠的结果),则称该方法是数值稳定的;出现与数值稳定相反的情况,则称之为数值不稳定的。(蝴蝶效应?)
* 例如:

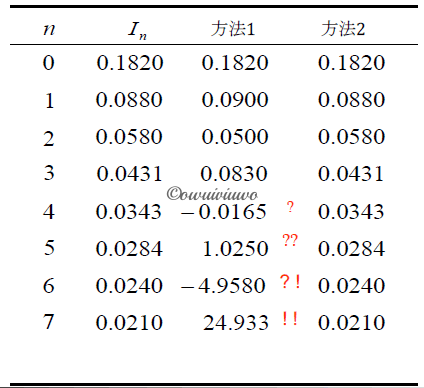

可见,两种方法计算得到的误差是有显著区别的。方法一每次都会使误差放大5倍;方法二每次都会使误差缩小为原来的 $\frac{1}{5}$。递推计算多次后就会有相当大的差别。而事实上方法一符合通常的思路,因为方法一的起点是已知的;而方法二的起点是未知的,计算难以开始。
一种可能的思路是,由积分中值定理可知,显然积分的结果在 0-1 之间,那不妨假设 $I_{15}=\frac{1}{2}$,并以此利用方法二反推得到 $I_7$,这样最后递推计算 8 次后,误差被缩小为原来的 $(\frac{1}{5})^8$,这对于 0-1 之间的结果来说是可以接受的,或者可以取大于 15 的数字开始递推更多次,使得误差被进一步缩小。
避免误差危害的基本原则
- 避免有效数字的损失
- 避免计算机上出现的”大数吃小数“
例如:

- 利用求根公式求解一元二次方程时,若 b 远大于 ac 的积,则 $\sqrt{b^2-4ac}\approx|b|$,分母中的 $-b\pm\sqrt{b^2-4ac}\approx0 $, 出现了两相近的数相减的情况。
其例子与解决方法如下:



- 避免小数作除法或大数作乘数
- 减少运算次数
- 使用秦九韶算法
例如求 $p_n(x)=a_nx^n+a_{n-1}x^{n-1}+\cdots+a_1x+a_0$ 的值,可通过如下过程:
$\begin{aligned}p_n(x)&=a_nx^n+a_{n-1}x^{n-1}+\cdots+a_1x+a_0\\&=(a_nx+a_{n-1})x^{n-1}+\cdots+a_1x+a_0\\&=((a_nx+a_{n-1})x+a_{n-2})x^{n-2}+a_{n-3}x^{n-3}+\cdots a_1x+a_0\\&=\cdots=\\&=((\cdots((a_nx+a_{n-1})x+a_{n-2})x+\cdots+a_{2})x+a_1)x+a_0\end{aligned}$
相较于直接逐项求和计算需要的 $2n-1$ 次乘法,使用秦九韶算法后,仅需要计算总共 $n$ 次乘法即可得到所需的结果。
例如:$P_5(x)=5x^5+x^3-3x^2+x-1$
$\begin{aligned}P_5(x)&=5x^5+x^3-3x^2+x-1\\&=5x^5+0x^4+1x^3-3x^2+x-1\\&=((((5x+0)x+1)x-3)x+1)x-1\end{aligned}$
- 使用泰勒展开

1.3 向量与矩阵范数
范数的概念是复数模的概念的自然推广
向量范数
条件
对任意向量 $x$ 和 $y$ 及复数 $a\in C$,$f(x)=||x||$函数满足以下三个条件:
非负性
$||x||\geq0, ||x||=0 \Leftrightarrow x=0_{n\times1}$
齐次性
$||ax||=|a|\cdot||x||$
三角不等式
$||x+y||\leq||x||+||y||$
称函数 $||*||$ 为 上的一个向量范数,是连续函数
常用的向量范数
p-范数
$||x||_p=(\sum^n_{i=1}|x_i|^p)^{1/p}, 1\leq p<+\infty$
特别的,
$p=1, ||x||_1=(\sum^n_{i=1}|x_i|)$,$|x_i|$ 表示 $x_i$ 的模
$p=2, ||x||_2=(\sum^n_{i=1}|x_i|^2)^{1/2}=\sqrt{x^Hx}=\sqrt{(x,x)}$,其中 $x^H$ 表示 向量$x$ 的共轭转置
$p=+\infty, ||x||_\infty=\max_\limits{ 1\leq i\leq n}|x_i|$
向量加权范数

* 例如

等价性定理:
设 $||\cdot||_\beta$ 和 $||\cdot||_\alpha$ 为 $C^n$ 上的任意两种向量范数,则存在两个与向量无关的正常数 $c_1>0, c_2>0$,使得 $c_1||x||_\beta\leq||x||_\alpha\leq c_2||x||_\beta$,并称 $||\cdot||_\beta$ 和 $||\cdot||_\alpha$ 为 $C^n$ 上的等价范数。
这一定理指出了尽管不同范数的值不一定相同,但都可以对向量进行度量。
特别的,
$||x||_\infty\leq||x||_1\leq n||x||_\infty$
$\frac{1}{\sqrt{n}}||x||_1\leq||x||_2\leq||x||_1$
$\frac{1}{\sqrt{n}}||x||_2\leq||x||_\infty\leq||x||_2$
或者
$||x||_\infty\leq||x||_2\leq||x||_1\leq\sqrt{n}||x||_2\leq n||x||_\infty$
矩阵范数 (m, F)
矩阵可以看(拉)做一个向量,可以把向量范数的概念直接推广到矩阵上
条件
对任意矩阵 $A$ 和 $B$ 及复数 $a\in C$ ,函数 $f(A)=||A||$ 满足以下四个条件:
非负性
$||A||\geq0, ||A||=0\Leftrightarrow A=0$
齐次性
$||\alpha A||=|\alpha|\cdot||A||$
三角不等式
$||A+B||\leq||A||+||B||$
相容性
相比于向量范数,矩阵范数应考虑到矩阵乘法。
对任意矩阵 $A\in C^{m\times l}$,$B\in C^{l\times n}$,满足 $||AB||_{M1}\leq||A||_{M2}\cdot||B||_{M3}$
满足非负性、齐次性、三角不等式、相容性的函数 $|| ||$ 称为矩阵范数
对于矩阵 $A_{m\times n}$,常见的矩阵范数有:
$m_1$ 范数,$||A||_{m_1}=\sum^m_{i=1}\sum^n_{j=1}|a_{ij}|$;
$F$ 范数,$||A||_F=(\sum^m_{i=1}\sum^n_{j=1}|a_{ij}|^2)^{1/2}$;
$m_\infty$ 范数,$||A||_{m_\infty}=\sqrt{m\cdot n}\cdot\max\limits_{ij}|a_{ij}|$;
注意 $||A||_{m‘_\infty}=\max\limits_{ij}|a_{ij}|$ 不构成 $A$ 的范数,理由如下图所示:

矩阵范数的等价性定理:设 $||\cdot||_\beta$ 和 $||\cdot||_\alpha$ 为 $C^{n\times n}$ 上的任意两种矩阵范数,则存在两个与矩阵无关的正常数 $c_1>0, c_2>0$,使得 $c_1||A||_\beta\leq||A||_\alpha\leq c_2||A||_\beta$,并称 $||\cdot||_\beta$ 和 $||\cdot||_\alpha$ 为 $C^{n\times n}$ 上的等价范数。
矩阵范数的性质
定义:
称集合 $\sigma(A)=\{\lambda|\det(\lambda I-A)=0\}$ 为矩阵 $A\in C^{n\times n}$ 的谱;也就是 $A$ 的所有的特征值全体;
称实数 $\rho(A)=\max|\lambda|$ 为矩阵 $A\in C^{n\times n}$ 的谱半径;也就是 $A$ 的绝对值最大的特征值;谱半径不是矩阵的范数。

三个重要定理
定理1:设 $|| \cdot ||_M$ 为矩阵 $C^{n\times n}$ 空间的任一矩阵范数,则对任意的 $n$ 阶方阵 $A$ 均有 $\rho(A)\leq||A||_M$,其中 $\rho(A)\leq||A||_M$ 为 $A$ 方阵的谱半径
证明:

定理2:对于任给的 $\varepsilon>0$ ,则存在 $C^{n\times n}$ 上的一种算子范数 $|| ||_M$ (依赖矩阵 $A$ 和常数 $\varepsilon$),使得 $||A||_M\leq\rho(A)+\varepsilon$;
注意:对另一矩阵 $B$,不等式不一定成立
定理3: 设 $A\in C^{n\times n}$ ,如果有 $C^{n\times n}$ 上的一种矩阵范数 $||\cdot||$,使得 $||A||<1$ 则
(1)$ I\pm A$ 可逆;
(2)$||(I\pm A)^{-1}||\leq\frac{||I||}{1-||A||}$;
(3)$||I-(I\pm A)^{-1}||\leq\frac{||A||}{1-||A||}$;
注:如果 $\lambda_i, i=1,2,\cdots,n$ 是矩阵 $A$ 的特征值,则矩阵 $I\pm A$ 的特征值为 $\mu_i=1\pm\lambda_i, i=1,2,\cdots,n$
证明:


算子范数
由于矩阵与向量的乘积在矩阵计算中经常出现,所以希望矩阵范数与向量范数之间最好有某种协调性
相容性
矩阵范数与向量范数的相容性的定义: 对矩阵范数 $|| ||_M$ 与向量范数 $|| ||_V$,有 $||Ax||_V\leq||A||_M||x||_V$
显然,不是任意的矩阵范数与任意的向量范数相容。
结论:
- 矩阵 m1-范数与向量 p-范数相容,即 $||Ax||_P\leq ||A||_{m1}||x||_p$
- 矩阵 F-范数与向量 2-范数相容,即 $||Ax||_2\leq||A||_F||x||_2$
- 对任一矩阵范数均存在与之相容的向量范数
定理1.4(算子范数定义):已知 $C^m$ 和 $C^n$ 上的同类向量范数 $||\cdot||_V$,$A$ 为 $m\times n$ 矩阵,定义 $||A||_M=\max\limits_{x\neq0}\frac{||Ax||_V}{||x||_V}=\max\limits_{||x||_V=1}||Ax||_V$,则 $||A||_M$ 是一种矩阵范数,且与已知的向量范数相容。
对于矩阵 $A_{m\times n}$,常用的算子范数有
列和范数:$||A||_1=\max\limits_{1\leq j\leq n}\sum_{i=1}^m|a_{ij|}$
行和范数:$||A||_\infty=\max\limits_{1\leq i\leq m}\sum^n_{j=1}||a_{ij}||$
谱范数:$||A||_2=\sqrt{\lambda_\max(A^HA)}=\sqrt{\rho(A^HA)}$,(谱半径开根号)
可以证明:$||A||^2_2\leq||A||_1||A||_\infty$
其中 $\lambda_\max(A^HA)$ 表示矩阵 $A^HA$ 的最大特征值;(或 $\sqrt{\rho(A^HA)}$)
特别的,$||A||_{m_1}$、$||A||_F$ 不是算子范数
(下标带 m、F 的是矩阵范数,其他的是矩阵范数中的算子范数?)
* 例如1
针对单位矩阵

* 例如2

*酉矩阵的范数不变性
对于酉矩阵 $U, U^HU=UU^H=I$,(该矩阵与其共轭转置的乘积为单位矩阵),
有 $||U||_2=1, ||AU||_2=||UA||_2=||A||_2$;
推导过程如下:

*F-范数的酉不变性
设 $A$ 为 $n$ 阶方阵,则存在 $n$ 阶酉阵 $U$ 和 $V$, 使得 $||UA||_F=||AV||_F=||UAV||_F=||A||_F$
推导过程如下:

其他的结论